Matías, hombre paciente

Acertijo de fin de año

Como felicitación navideña, les presento la versión que Vince Guaraldi hizo de O Tannenbaum para una película sobre Charlie Brown y Snoopy. Aquí está magníficamente tocada al piano por mi amigo Fernando, que es como amigo aún mejor que como pianista. Gracias, Fernando. 

Una vez más Escher me ilustra un post.

No hay que perder las buenas costumbres. Y habida cuenta de las pocas costumbres que tiene este blog anárquico y esporádico, cualquiera de la que dé la menor muestra debe ser considerada y alentada como una buena costumbre. Así pues, como llevo ya por lo menos... uno o dos años ofreciendo a mis trece lectores, por estas fechas, un enigma para que entretengan sus ocios navideños, he decidido continuar la tradición un fin de año más. 

Esta vez, sin embargo, no se trata de uno de los Problemas Exactos al margen de las Matemáticas de mi tío Guillermo, sino de otro producto del ingenio familiar. (Estos días son muy familiares, ya saben ustedes). Uno de mis hermanos compuso hace ya tiempo el ingenioso problema que a continuación les ofrezco. Vean ustedes si tienen ganas de leerlo, estudiarlo y dar respuesta a las cinco sencillas preguntas en que se centra la cuestión. Si es el caso, pueden ustedes enviar sus soluciones a cualquiera de las siguientes direcciones:

ohvanbrughARROBAgmailPUNTO com

o bien

jubilomatinalARROBAgmailPUNTOcom

cambiando en la que vayan a emplear, claro está, la palabra ARROBA por el simbolillo @ correspondiente, y la palabra PUNTO por un punto . propiamente dicho.

El premio, naturalmente, será la satisfacción que produce el buen funcionamiento del propio aparato razonador, tanto mientras se ejercita como después, cuando se contemplan sus frutos.

La solución, también como de costumbre, la traerán los Reyes si son ustedes buenos.

¡Feliz Navidad a todos!

He aquí el PROBLEMA:

Matías, hombre paciente, ha construido un conjunto de piezas con las siguientes características: 

 - Las hay de dos estructuras: macizas y huecas.

 - Las hay de dos colores: blancas y negras.

 - Las hay de dos formas: cúbicas y esféricas.

 - Las hay de dos tamaños: grandes y pequeñas.

 - Las hay de dos materiales: metal y madera.

 - Las hay de dos precios: caras y baratas. 

En el conjunto existen todas las combinaciones posibles, pero no hay dos iguales. 

Los tres mejores amigos de Matías: Antonio, Benito y César, tienen extrañas manías, debido a traumas psíquicos de la niñez: 

 - Antonio no puede ver las esferas, salvo si son de madera. Además no le gusta el color negro ni los objetos huecos.

 - Benito colecciona cubos y aborrece las cosas pequeñas, excepto si son macizas.

 - César odia los metales y es alérgico a las maderas caras. 

Suponiendo que cada uno de ellos se llevó todas las piezas que quiso, de acuerdo con sus gustos, fobias y manías, y que eligieron por orden alfabético, debemos averiguar: 

1º ¿Cuántas piezas se llevó Benito que habría querido César? 

2º De estas ¿es alguna cara? 

3º ¿Cuántas piezas le quedaron a Matías? 

4ª ¿Cuál de los datos que hasta ahora hemos dado se hubiera podido suprimir sin que variaran en nada las tres primeras respuestas? ¿Por qué?

5º Transcurridos cien años, la colección de piezas, fragmentada en la forma que hemos visto, se encuentra en manos de los únicos nietos de Matías, Antonio, Benito y César, respectivamente. Sin embargo éstos no han heredado las fobias, las manías ni los gustos de sus ancestros. El nieto 1, que se llama igual que su abuelo y posee el cubo de madera, grande, negro, macizo y barato, querría entrar en contacto con el nieto 2, también homónimo de su antepasado, que guarda el cubo caro, grande, macizo, metálico y blanco, para proceder a un intercambio. ¿Cuáles son los nombres de los nietos 1 y 2?

El extraño caso del primer dígito. Parte III



El gráfico está tomado de un artículo  sobre el fenómeno del primer dígito publicado en 2007 por cuatro físicos de la Universidad de Córdoba⁽¹⁾ en el European Journal of Physics. Las cinco barras representan las frecuencias de cada dígito en el primer puesto de las cifras de datos de las siguientes cinco magnitudes; Variaciones anuales del IPC español, Poblaciones de los 8.107 municipios españoles en el último censo, Aves existentes en las distintas regiones españolas entre 1975 y 2002, Áreas en km2 de los países del mundo y Datos contables anuales de una empresa. Los rombitos blancos son las frecuencias de cada dígito en el primer puesto de los números premiados por la lotería española desde 1995. (Todos los datos están tomados del INE). Los puntos negros unidos por una curva, por último, son las frecuencias predichas por la Ley de Benford.

Recapitulemos:

Acababa mi anterior post sobre este asunto tan interesante como popular resumiendo mis perplejidades en tres preguntas fundamentales que, en mi opinión, se plantean ineludiblemente a cualquiera que se interese por el Extraño Caso del Primer Dígito:

1º ¿En qué se diferencian los fenómenos cuyos datos numéricos se ajustan a la Ley de Benford de aquellos otros que producen también cifras, pero ateniéndose a la ley de probabilidades monda y lironda, es decir, sin esa sorprendente distribución de frecuencias de su primer dígito que caracteriza a los primeros?

2º ¿Qué tienen en común entre sí los variadísimos fenómenos que sí se atienen, todos ellos, a la distribución logarítmica del primer dígito de sus datos numéricos? Y

3º ¿Por qué son más frecuentes los datos numéricos con primeros dígitos bajos que los que los tienen altos, y por qué en esa proporción?

Mi propósito es dedicar este tercer y último post de la serie a comentar lo más brevemente que pueda cada una de estas preguntas y las reflexiones a que me han dado ocasión, a las que sería más bien iluso llamar respuestas.


Unos sí y otros no. Qué cosas.

Estos días que llevo dándole vueltas al asunto y leyendo sobre él todo lo que cae en mis manos, me he encontrado hasta la saciedad la expresión "fenómenos que se presentan en el mundo real". Todo el que trata de la Ley de Benford recurre a esta expresión como si se tratara de una condición fundamental para que se cumpla la bendita ley, pero lo cierto es que yo no sé de ningún fenómeno que no se produzca en el mundo real, por lo que en principio no me parece que la expresión en cuestión sea de mucha utilidad. Los sorteos, los catálogos, los fraudes contables y los experimentos amañados son todos ellos fenómenos que también tienen lugar en el mundo real y, sin embargo, parece ser que las cifras que resultan de ellos no se atienen a la ley de Benford.

Como para casi todo en este asunto, yo he encontrado lo que me parece la clave en las dos paginitas publicadas por el pobre Newcomb en 1881, de las que nadie hizo ni caso en su momento.

"Tal como los números naturales se presentan en la naturaleza, escribe Newcomb, deben ser considerados como proporciones entre cantidades" . (Las negritas, como siempre, son mías. Les tengo afición).

Ese es el asunto, a mi entender. Las cifras distribuyen de un modo inesperado sus primeros dígitos solamente cuando expresan cantidades. Un número premiado en la lotería, un código numérico asignado a un elemento en un catálogo (números de teléfonos, Clasificación Decimal Universal de documentos, ISBN, números de identidad o de Seguridad Social...) o unos datos inventados para engañar a Hacienda son, todos, cifras que no se refieren a ninguna cantidad de ninguna magnitud medible de ninguna cosa existente. No son el resultado de una medición, y por eso Benford no tiene nada que ver con ellas. Solo las cifras que se han obtenido midiendo magnitudes cuantificables de cosas existentes son las que presentan primeros dígitos con una frecuencia logarítmica, y no equitativamente repartida entre las nueve posibilidades. Da lo mismo que se trate de áreas, de precios, de poblaciones, de alturas o de distancias. Da igual que lo medido sea obra de la naturaleza o del hombre. Lo que hace que una serie de cifras presente una distribución de primeros dígitos con arreglo a la Ley de Benford es, en mi opinión, el hecho de que esas cifras sean el resultado de medir cualquier magnitud cuantificable de cualquier cosa realmente existente, desde el número de camellos en los desiertos asiáticos hasta el de partículas nucleares en los compuestos químicos, pasando por el de ladrillos en los edificios construídos en la Expo lisboeta y por el de licencias de taxi concedidas en las ciudades centroeuropeas. Da igual qué se mida, lo importante es que algo se mide y que el resultado de la medición se expresa en números.

Y hay que hacer notar a este respecto la estupenda precisión de Newcomb, que no habla solo de cantidades, sino de proporciones (ratios) entre al menos dos cantidades; y que, a partir de ahí, desarrolla en cinco o seis párrafos largos y abstrusos toda su explicación matemática del asunto: "Por eso, sigue diciendo tras la frase citada arriba, en vez de tomar un numero al azar, debemos tomar dos y preguntarnos cuál es la probabilidad de que el primer dígito significativo de su cociente (ratio) sea n". Sea uno o no capaz de comprender el razonamiento matemático que sigue a este planteamiento, lo que sí es fácilmente comprensible es que cualquier medición, efectivamente, es siempre una proporción entre dos cantidades, la cantidad que se mide y la que se emplea como unidad de medición. La altura de una montaña es la que es, pero no tenemos ninguna cifra para expresarla hasta que, además de esa altura, tomamos otra para usarla como unidad, y establecemos la proporción entre ambas, que es la que nos da la cifra con que expresamos esa altura. Lo que hace Newcomb al hablar de proporciones entre dos cantidades es hablar de mediciones y situar la cuestión, desde el principio, en el terreno en el que yo creo que debe ser planteada.


Si cada uno es de su padre y de su madre...

... ¿qué pueden entonces tener en común fenómenos tan absolutamente distintos entre sí como, por ejemplo, los del gráfico que encabeza el post, y otros muchísimos que cada día se comprueba que producen series de datos con los primeros dígitos distribuidos según la Ley de Benford?

También sobre esta cuestión he leído las respuestas más sorprendentes –y las afirmaciones más obvias y anodinas, que sorprendentemente, se presentaban a sí mismas como respuestas–. Desde el matemático francés que, tras analizar sesudamente los aspectos más técnicos de la distribución de Benford, la justifica despreocupadamente con la hipótesis de que nuestra tendencia a pensar que todos los dígitos se han de repartir por igual el primer puesto es simplemente un condicionamiento psicológico sin ninguna otra base que la intuición –¡ahí queda eso!–, hasta los físicos chinos que están convencidos de que la Ley de Benford es algo parecido a una nueva ley de la gravitación universal, y obedece a la existencia de una constante universal, subyacente bajo la esencia misma de todo lo existente que, cuando sea descubierta y estudiada, nos ayudará a encontrar las explicaciones que aún no tenemos sobre la estructura subatómica de la materia. Lamento decir que ninguna me ha convencido, ni me ha parecido siquiera nada remotamente similar a una explicación sensata y aceptable del asunto.

Mi opinión personal es que los fenómenos que producen datos numéricos con la frecuencia de sus primeros dígitos distribuída según la Ley de Benford no tienen absolutamente nada en común, ni falta que les hace.

Nada, salvo el hecho de que los medimos, el resultado de lo cual expresamos en cifras.

Dicho de otro modo: en mi opinión, la de producir series de datos numéricos que empiezan más frecuentemente por números bajos que por números altos, todas ellas más o menos aproximadas a las frecuencias que para el primer dígito nos da la Ley de Benford, no es una propiedad de los fenómenos medidos, sino del sistema numérico con el que expresamos los resultados de nuestras mediciones. Ni en los ríos, ni en las aves, ni en el IPC, ni en los camellos asiáticos, ni en los compuestos químicos ni en los taxis rumanos hay nada que les lleve a distribuir sus cantidades de determinada manera. De hecho ninguna de estas cosas distribuye sus cantidades de ninguna manera. Somos nosotros los que, para referirnos a esas cantidades, a todas las cantidades, les asignamos cifras con arreglo a un sistema numérico que es el único lugar en el que se produce el fenómeno del primer dígito.

En la naturaleza no hay números. Los números son una convención artificial y arbitraria que solo existe en nuestras cabezas. Un lenguaje. Atribuir a las cosas concretas una cualidad que solo aparece en los números con que las cuantificamos tiene exactamente el mismo fundamento que atribuir a las vacas las particularidades de la palabra "vaca". Ni las vacas se escriben con V, ni los ríos tienen longitudes con los primeros dígitos distribuídos según la Ley de Benford. Tanto la de comenzar por una u otra letra como la de distribuir los primeros dígitos de uno u otro modo son propiedades de las palabras y de las cifras, no de las cosas a las que se refieren. De los lenguajes con que nos referimos al universo, no del universo mismo.

¿Por qué precisamente el 30'1 %, vamos a ver? ¿Por qué estos valores, y no otros?

Ya situados estrictamente en el terreno al que creo que debe ceñirse la cuestión: el de nuestro sistema numérico, y no el de las cantidades para expresar las cuales lo usamos, y mucho menos el de los fenómenos a que se refieren esas cantidades, sigue siendo intrigante una cuestión: ¿por qué nuestro sistema numérico, cuando lo usamos para expresar cantidades de magnitudes de cosas existentes, tiende a producir números comenzados por 1 y por 2 con más abundancia que números comenzados por 8 y por 9? Y ¿por qué en esas proporciones precisas, y no en otras?

Porque una cosa seguimos teniendo clara, y es que, en el conjunto de TODOS nuestros números, todos los dígitos significativos (es decir, despreciando los ceros iniciales de los decimales) aparecen como primero con la misma frecuencia. Hay tantos números empezados por 1 como por 2, por 3... y por 9. Y lo mismo sucede cuando consideramos tramos redondos de este conjunto: los cien primeros, los mil primeros, los mil millones primeros... los 10⁸⁰ primeros. Por eso funcionan las loterías, decíamos hace un par de posts.

Pero la cosa deja de suceder si los tramos considerados no son "redondos", esto es, si no terminan en potencias exactas de 10. Si consideramos los quince mil millones primeros de números, por ejemplo, en los diez mil primeros millones los nueve dígitos se reparten el primer puesto equitativamente, pero en los cinco mil millones siguientes todos los números empiezan por 1, lo que altera considerablemente la frecuencia con la que el 1 aparece como primer dígito en ese tramo concreto y, por tanto, la probabilidad de que una cifra cualquiera de ese tramo empiece por 1.

Sucede lo mismo, o más aún, en los quince primeros números, en los ciento setenta primeros números, en los mil novecientos primeros números, en los un millón novecientos mil primeros números... En todos estos tramos la frecuencia con la que el 1 es el primero de una cifra cualquiera es muy superior a 1/9.

En nuestra cabeza y en nuestros bombos de lotería⁽²⁾–valga decir, en cualquier proceso de obtención de cifras que no sea resultado de la medición de algo existente– consideramos tramos redondos de números, tramos terminados en potencias de 10, los únicos en que los nueve dígitos tienen la misma probabilidad de comenzar una cifra cualquiera. Pero las magnitudes de los fenómenos que suceden en el mundo real no toman esa precaución. Ni cuentan con TODOS los números, porque el universo y todo lo que hay en él es finito, ni ajustan sus dimensiones a tramos "redondos" de números, que acaben en potencias de 10. Entre otras cosas porque, como ya hemos dicho, en el mundo de fuera de nuestras cabezas no hay números, solo cantidades, a las que nuestro sistema numérico y nuestra base 10 les importan un pito. Las cantidades son las que son, cómo las expresemos es asunto exclusivamente nuestro, del que el Universo pasa olímpicamente.

Y en un tramo cualquiera de números, un tramo que no acabe en una potencia de 10, la frecuencia con que cada dígito ocupa el primer puesto de las cifras ya no es igual para todos, como hemos visto.

Parece, por eso, que investigar cómo varía la frecuencia, en distintos tramos de números, de cada dígito como ocupante del primer puesto, puede ser una vía prometedora de investigación. 

Veamos, pues, dónde nos lleva con el 1, por ejemplo:

Si consideramos, de todos los números, solo el primero (que como es notorio es nuestro querido 1), la frecuencia con la que el 1 es el primer dígito de ese número es, evidentemente, del 100 %. Solo está él...

Si vamos ampliando el tramo de números considerados, va disminuyendo la frecuencia con la que el 1 es el primer dígito. Para el tramo de los dos primeros números, [1, 2], la frecuencia del 1 como primer dígito es del 50% (1/2). Para el tramo de los tres primeros, [1, 3], del 33'33 %, (1/3). Para el tramo de los cuatro primeros, [1, 4], del 25 %(1/4)...y así la frecuencia del 1 como primer dígito sigue bajando hasta que consideramos el tramo de los nueve primeros números, [1, 9], en el que la frecuencia del 1 como primer dígito es del 11'11 % (1/9).

Al ampliar el tramo en uno más y considerar los diez primeros números, [1, 10], la frecuencia del 1 como primer dígito vuelve a subir. Aquí ya hay dos números, el 1 y el 10, que tienen al 1 como primer dígito, luego la frecuencia es de 2/10, el 20 %. Conforme vamos ampliando el tramo considerado con los sucesivos números, va aumentando la frecuencia de números empezados por 1. Es del 27'27 % (3/11) en el tramo [1, 11], del 33'33 % (4/12 = 1/3) en el tramo [1, 12], del 38'46 % (5/13) en el tramo [1,13]... hasta llegar al tramo [1, 19], en el cual hay 11 números que empiezan por 1, es decir que su frecuencia alcanza el 57'89 % (11/19). Pero en el tramo [1, 20] baja al 55 % (11/20), en el tramo [1, 21] es del 52'38 % (11/21)... y sigue bajando al ampliarse los tramos: 36'66 %(11/30) en el [1,30], 27'5 % (11/40) en el [1, 40]... hasta que en el [1, 99] es de nuevo del 11'11 % (11/99).

Para empezar de nuevo a subir en el [1, 100] (12/100 = 12 %) y seguir subiendo hasta la del tramo [1,199] (111/199 = 55'77 %), desde el que vuelve a bajar incesantemente hasta volver a ser del 11'11 % = 111/999 en el tramo [1, 999]. Y así todo el rato. 

Por resumir, la gráfica que dibuja la frecuencia del 1 como primer dígito en los sucesivos tramos, –cada uno con diez veces más números que el anterior aunque yo los haya dibujado en una escala en la que aparecen todos iguales porque, si no, no me cabe y el principio es el mismo–,  viene a ser algo así:

Sobre el eje vertical se representan las frecuencias en % con las que el 1 es el primer dígito de una cifra en los tramos de cifras [1, n] representados sobre el tramo horizontal. Este último está dibujado a escala logarítmica, en la que se representa con la misma longitud el tramo [1.000, 10.000] que el [100, 1.000 y que el [10, 100]... Es decir, todos los tramos aparecen con la misma longitud,, a pesar de que cada uno es, en realidad, de una longitud igual a diez veces la del anterior.

La serie se prolonga indefinidamente hacia la derecha, con la frecuencia con la que aparece el1 como primer dígito oscilando en cada nuevo tramo entre dos límites, inferior y superior que, aunque en el gráfico no se advierta, no son siquiera constantes. El límite inferior va decreciendo hacia el valor 1/9 = 0'1111 (11/99,  111/999,  1.111/9.999...) y el superior también decrece hacia 5/9 =0'5555 (11/19,  111/199,  1.111/1.999...). A efectos prácticos podemos considerar que oscila periódicamente entre el 11'11 % y el 55'55 % (las variaciones entre los límites de un tramo y los del siguiente empiezan a la altura del tercer decimal, y de ahí en adelante son cada vez más pequeñas).

Y también a efectos prácticos parece que sería útilpoder establecer un valor promedio de esta sucesión de frecuencias, el valor hacia el que tiende –o en torno al cual oscila, en este caso– la frecuencia con la que el 1 es el primer dígito, a medida que el extremo derecho de los sucesivos tramos avanza interminablemente hacia el infinito. Lo que matemáticamente se llama el límite de la sucesión.

Mis habilidades matemáticas, que no son ya lo que alguna vez fueron y nunca fueron gran cosa, no se acercan siquiera a poder calcular el límite de una sucesión así. Me consuela que A. Jamain⁽³⁾, que parece saber de lo que habla y pertenece al Imperial College of London, donde nunca dicen nada solo por decir, tras asegurar que tal límite no existe, suaviza la negativa (¡cómo disfrutan los matemáticos dándonos estos sustos!) diciendo que hay diversos métodos para definirlo, y que varios de ellos llevan al deseadologaritmo de 2, que vale, precisamente, 0'3010 (o 30'1 %), el valor de la probabilidad del 1 como primer dígito según la Fórmula de Newcomb (log (1+1/1), si recuerdan ustedes), fórmula que es, a su vez, la expresión matemática de la Ley de Benford. ¡Menos mal!

Con tal autorización me siento más libre de aventurar mi propia cuenta de la vieja explicativa, que a mí al menos me sirve para entender mejor la cuestión. Si coloreamos el espacio bajo la curva del anterior gráfico, tal que así:

el área coloreada parece bastante razonablemente asimilable –los picos que entran por los que salen, ya me entienden ustedes– a la del rectángulo así mismo coloreado en este otro gráfico; rectángulo cuya base es la misma y cuya altura he situado, así, por ver qué pasa, a la altura de... pongamos por caso... el 30'1 %:

Lo que a mi ojo de buen cubero geómetra le viene a decir que la oscilación de la frecuencia del primer dígito 1entre sus dos límites viene a ser como si se mantuviera todo el rato en ese valor de 30'1 %  (o 0'3010), que es, no hace falta decirlo, la deseada probabilidad del 1 como primer dígito que nos daba la fórmula de Newcomb, o sea, quod erat demostrandum. ¿Me he explicao?

(Supongo que la cosa se podría comprobar con un poco más de rigor haciendo la integral de la curva entre dos puntos suficientemente alejados, lo que nos daría el área picuda, y dividiéndola luego por la distancia entre esos dos puntos para que nos saliera la altura del rectángulo equivalente, que es el valor buscado y al que más le vale seguir entonces siendo lo más parecido que pueda a 0'3010. Pero para eso tendría que conocer la ecuación de la curva y recordar cómo se resolvían integrales. Dios lo haga mejor. Se lo dejo a Jamain, que sabe mucho. Yo me conformo con mi heurística doméstica).


Naturalmente, el razonamiento es generalizable a todos los demás dígitos: de los nueve mil primeros números, solo el 1'25 % empieza por 9. Y lo mismo sucede en los nueve primeros millones, en los novecientos mil primeros millones...

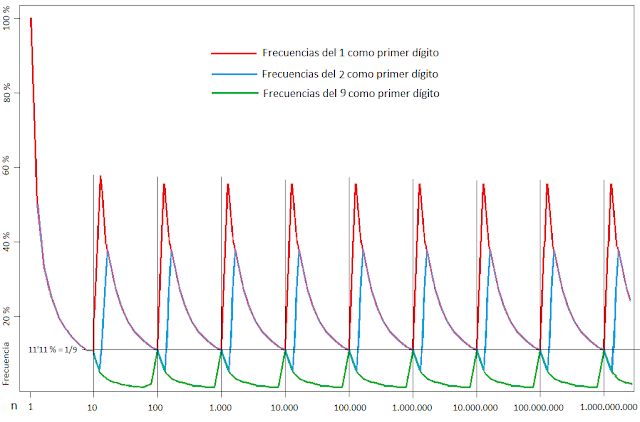
Si trazamos para el 2 y el 9, por ejemplo, gráficas similares a las que hemos trazado para el 1, nos quedará algo parecido a esto (las del 2 en azul y las del 9 en verde):

Como se ve, las dos frecuencias, la del 2 como primer dígito y la del 9 en ese mismo puesto, oscilan, igual que lo hacía la del 1, en torno a sendos valores promedios –los límites respectivos de ambas series–, que, tanto de acuerdo con mi ojímetro geométrico como –o al menos eso espero– con los sabios métodos de integración de A. Jamain, pueden situarse, respectivamente, en las alturas del 17'6 %  la del 2 (la frecuencia que la fórmula de Newcomb nos daba para el 2 como primer dígito) y del 4'58 %  la del 9 (la frecuencia que la fórmula de Newcomb nos daba para el 9 como primer dígito).

Resulta muy interesante, para terminar, superponer las tres curvas en un solo gráfico, en el que es fácil comprobar que las frecuencias con que cada uno de estos tres dígitos son el primero de una cifra solo coinciden para valores de n iguales a potencias exactas de 10 (10, 100, 1.000, 10.000..), en los que las tres frecuencias se encuentran a la altura del 11'11 % (1/9)

Con lo cual considero dicho todo lo que me apetecía decir sobre el asunto. No creo, naturalmente, haber contestado ninguna de mis tres preguntas, pero sí he conseguido que se me pasen las ganas de seguir planteándomelas, lo que en la práctica es bastante equivalente. Podemos descansar, por tanto, que bien nos lo hemos ganado.


Notas:

(1) How do numbers begin? (The first digit law) J. Torres, S. Fernández, A. Gamero y A. Sola. European Journal of Physics, 24 April 2007.

(2) En realidad en los bombos de lotería no es necesario hacerlo, y de hecho en el de Navidad no se hace, ya que de lo que se trata no es de acertar el dígito inicial, sino el número completo, y los números completos tienen todos la misma probabilidad sea cual sea el tramo elegido.

(3) Benford's Law Adrien Jamain  Imperial College of London, Department of Mathematics. April - September 2001

El extraño caso del primer dígito. Parte II

Los logaritmos estaban en el ajo desde el principio.

En un librillo parecido a este debió
de hacer Newcomb su observación.

No sé si los estudiantes de bachillerato siguen estudiando logaritmos, pero lo que es seguro es que ya no se usan habitualmente para calcular, que fue su utilidad primera. Las calculadoras y los ordenadores han hecho que las tablas de logaritmos cuyo manejo aprendí yo a eso de los quince años hayan quedado tan obsoletas como las reglas de cálculo, que eran, por cierto, unos objetos francamente bonitos. Pero hace ciento y pico años –y también hasta hace relativamente poco– estas tablas eran una herramienta de trabajo habitual de ingenieros, físicos, biólogos, sociólogos, astrónomos y cualquiera que tuviera que hacer a diario cálculos matemáticos.

La pequeña historia que les voy a contar, en la que estos numeritos tan útiles y de nombre tan amenazadoramente griego juegan distintos y todos ellos importantes papeles, pueden encontrarla ustedes en cualquiera de las tropecientas páginas que les saltarán a la pantalla si teclean "Ley de Benford" en Google, porque nadie que se ocupe de esta Ley deja de empezar con ella sus consideraciones. Tampoco yo voy a poder evitarlo, aunque intentaré despachar el trámite con la mayor rapidez posible.

Simon Newcomb, con toda la barba

El caso es que en 1881 un astrónomo nacido en Canadá pero que trabajaba en EEUU, Simon Newcomb, constató que el librillo que recogía sus tablas de logaritmos tenía mucho más estropeadas las primeras páginas que las últimas. Por motivos técnicos que no hacen al caso –en realidad sí hacen bastante al caso, pero ya tiendo yo a enrollarme lo suficiente sin necesidad de que nos pongamos ahora a explicar qué es un logaritmo y cómo funciona; sobre todo porque aspiro a que sigan ustedes leyéndome– resulta que las tablas de logaritmos agrupan los números por sus dígitos iniciales, esto es, el logaritmo de 12, el de 145 y el de 1.718 deben buscarse en las páginas de las cifras que empiezan por 1; el de 57, el de 0'00521 y el de 5.133, en las de las que empiezan por 5...

Por lo cual, lo que Newcomb acababa de descubrir es que quienes usaban las tablas habían buscado en ellas muchas más veces el logaritmo de cifras empezadas por 1 y por 2, que estaban al principio, que el de cifras empezadas por 8 y 9, que estaban al final, en las páginas claramente más limpitas y menos usadas.

El buen Simon le dió vueltas al asunto, comprobó que el fenómeno se repetía en todas las tablas de logaritmos que cayeron en sus manos, y concluyó que, por algún motivo (como buen científico práctico no parece que le diera muchas vueltas a cuál podía ser ese motivo, se limitó a constatar que la cosa ocurría), las cifras empezadas por números bajos aparecían con mucha más frecuencia que las otras en los cálculos de los usuarios más diversos de tablas logarítmicas, o sea, en una gran variedad de campos distintos. Acabó por escribir un articulito –él lo llama "Nota"– sobre la cuestión, que publicó en el American Journal of Mathematics. En él, tras referirse brevemente a su observación, ("Que los diez dígitos no se presentan con igual frecuencia, empieza diciendo el artículo, debe resultarle evidente a cualquiera que haga mucho uso de las tablas de logaritmos y advierta cuánto más deprisa se desgastan las primeras páginas que las últimas. El primer lugar significativo lo ocupa el 1 más veces que cualquier otro dígito, y la frecuencia va disminuyendo hasta el 9". Y con eso daba por suficientemente presentada la cuestión) llegaba a la sorprendente conclusión de que la probabilidad de que uno cualquiera de los nueve dígitos ocupara el primer lugar significativo de una cifra no siempre valía para todos 1/9, como hasta ahora hemos convenido que era lo razonable. "Tal como los números naturales se presentan en la naturaleza, es decir, considerados como proporciones entre cantidades" (las negritas son mías), la probabilidad de un dígito de ocupar el primer puesto, según Newcomb, debía calcularse mediante la fórmula

Prob (1^er digito significativo = d) = log₁₀ (1+1/d)

Que, leída en cristiano, viene a decir que la probabilidad de un dígito cualquiera d de ser el primer dígito significativo de una cifra es igual al logaritmo decimal de 1 más 1 partido por d. 

O sea que, por si afirmar que la probabilidad de ser el primero no era la misma para todos los dígitos no fuera suficientemente chocante, se atrevió además a señalar cómo debía calcularse para cada uno.

(Como ven, los logaritmos, que parecía que solo por casualidad habían dado la primera señal de alarma sobre la existencia de este fenómeno, se instalaban ahora en el meollo del asunto, y con toda la pinta de llegar para quedarse. Lo que se llama una buena estrategia, con los tiempos bien medidos. Si eso no es premeditación, que venga Dios y lo vea).

La fórmula en cuestión no aparece así enunciada en el escrito de Newcomb, pero lo que sí contiene su trabajo es esta bonita tabla, cuya primera columna son los valores (frecuencias de cada dígito en el primer puesto) que resultan de sustituir en la fórmula d por 1, 2, 3,... ...,9 :

Esta tabla está directamente copiada de la Nota de Newcomb.
Creo que debería citar aquí no sé qué copyright, en la Nota lo dice...

En su segunda columna la tabla, habrán visto, presenta también la probabilidad de cada dígito de ocupar el segundo puesto de una cifra, y aquí ya sí entra el 0. Las frecuencias del segundo puesto siguen siendo decrecientes, empezando por la más alta del 0, pero con una diferencia entre ellas mucho menor, es decir, formando una curva mucho más "plana". "En el caso del tercer puesto la probabilidad será casi la misma para cada dígito, y para el cuarto y siguientes la diferencia (de frecuencias) será inapreciable".

 Este gráfico,  en cambio, es de este artículo de Adrien Jamain.
He probado a hacer el mío propio, pero este queda más bonito.

El artículo de Newcomb pasó ampliamente inadvertido. El hombre se murió en 1909 con una buena reputación como astrónomo, pero mucho más conocido por un oportuno artículo en el que demostraba que una máquina más pesada que el aire nunca podría volar, que publicó solo unos meses antes de que los hermanos Wright lo desmintieran contundentemente, que por ningún otro de sus numerosos trabajos. Así de dura es, a veces, la vida de los científicos. Descanse en paz.

La tumba de Newcomb, en el Cementerio Nacional de Arlington

El Nombre de la Cosa. La Ley de Benford, y Benford, propiamente dicho.

¿Qué probabilidad había de que Frank Albert Benford fuera
inmortalizado justo el día en que se había puesto esa corbata?

Nadie había hecho el menor caso del artículo del pobre Newcomb. No sé si él se descorazonó, pero los logaritmos no lo hicieron, y cincuenta y tantos años después lo intentaron de nuevo. (Para los logaritmos, que no empezaron a dar señales de vida hasta el XVII, el tiempo es mucho menos importante que para nosotros. No tienen prisa...)

Esta vez escogieron a un físico que trabajaba en la General Electric, un tal Frank Benford, que volvió a observar el desgaste desigual de las tablas de logaritmos y sacó de él la misma conclusión que Newcomb. No solo eso, sino que siguió el mismo razonamiento y llegó a la misma fórmula para calcular la probabilidad que cada uno de los nueve dígitos tiene de ser el primero significativo en una cifra.

(Todos las alusiones a este razonamiento que he leído en Internet lo califican de "breve y heurístico". Este último palabro viene a decir que no se trata de una demostración rigurosa, sino de un apaño de andar por casa, una especie de aproximación habilidosa que procede más bien por tanteo. Yo solo lo he leído en la versión de Newcomb y, entre que está en inglés y que se basa en el concepto de límite, que yo usé por última vez con cierta soltura hace cosa de treinta años, confieso que me ha resultado algo más hermético que heurístico. Digamos que he llegado a captarlo solo en sus líneas generales, tendré que leerlo más despacio. Y leerme también el de Benford, que ocupa veintidós páginas en vez de las dos escuetas del canadiense, a ver si su explicación queda un poquito más a mi alcance).

No he averiguado si Benford conocía la Nota de su predecesor. (T.P. Hill, en un recomendable artículo sobre el asunto, dice con circunspección que era "apparently unaware of Newcomb's paper", es decir, que nunca dio señales de conocerlo. El propio escrito de Benford comienza con la austera información de que "Se ha observado que las páginas de una tabla de logaritmos muy usada presentan evidencias de un uso selectivo de los números naturales". Las negritas son mías). En cualquier caso, fuera que redescubriera él solito la cuestión o que se inspirara solapadamente en el recóndito y decimonónico trabajo del otro, se lo curró mucho más. Como primera providencia, científico concienzudo, lo comprobó. Realizó lo que él mismo llamó "un esfuerzo para reunir datos del mayor número posible de campos, y para incluir una amplia variedad de tipos... ...El rango de los asuntos estudiados fue tan amplio como lo permitieron el tiempo y la energía". Dedicó, nos cuenta Hill, "varios años a reunir datos, y la tabla que publicó en 1938 en los Proceedings of the American Philosophical Society se basaba en 20.229 observaciones provenientes de conjuntos de datos tan diversos como áreas de ríos, estadísticas de la Liga Americana de baseball, pesos atómicos de elementos y cifras aparecidas en artículos del Reader's Digest." "La tabla de primeros dígitos significativos que resulta se ajusta  a la fórmula logarítmica, dice, sumamente bien". (Las negritas son mías).

El artículo de Benford debe de devengar aún
derechos de autor, y solo he podido descargarlo
gratis de aquí para catorce días, tras abrirme una
cuenta. Lo he pedefeado diligentemente página
por página, pero como imagen. Almacenarlo en
forma de texto, de momento, ha sido imposible.

Benford tuvo más suerte que Newcomb. La comunicación que en 1937 presentó a la American Philosophical Society ("The Law of Anomalous Numbers", Proceedings of the American Philosophical Society, Vol. 78 nº 4, March, 31, 1938, pp. 551-572) obtuvo toda la atención que nunca conocíó el artículo de su predecesor. Desde su publicación, el interés de los matemáticos, físicos y demás fauna científica por la Ley de Benford (que, por cierto, ha recibido ese nombre en cumplimiento de otra ley, la de Stigler, que afirma que ningún descubrimiento científico lleva el nombre de su primer descubridor; seguro que no fue Stigler el primero en darse cuenta de eso) no ha hecho más que aumentar, y actualmente se aplica con normalidad en muchos campos, desde el diseño de rutinas informáticas y de modelos predictivos de fenómenos hasta la detección de fraude fiscal. Los investigadores de los ámbitos más variados no hacen más que encontrar nuevas magnitudes y fenómenos cuyas mediciones se ajustan a la distribución de Benford, y los matemáticos demuestran incansablemente nuevas propiedades de la Ley.

Una de las más interesantes, por cierto, es la de ser invariante respecto de la escala, esto es, que si una serie de datos cumple la Ley cuando se los expresa en una unidad cualquiera, seguirá cumpliéndola si los datos se expresan en otra unidad diferente. Una lista de altitudes de ciudades  medidas en pies, o de precios de artículos en dólares, transformada respectivamente a metros o a euros, contendrá otras cifras completamente distintas, pero los primeros dígitos de estas nuevas cifras de metros o de euros se ajustarán a la Ley de Benford del mismo modo que los de la lista inicial de cifras en pies o en dólares.  (La mente de los matemáticos funciona de un modo tan peculiar, quiero decir tan distinto de cómo funciona la mía, que tienden a presentar esta invariancia de escala como si se tratara de una explicación de la Ley. Los teólogos medievales explicaban la para ellos obvia existencia de Dios con argumentos no muy distintos, me parece a mí. Pero este género de consideraciones es ya más bien objeto de mi próximo post).

Y otra de estas propiedades que no puedo dejar de citar es la de ser invariante respecto de la base de numeración. Lo que quiere decir que si una serie de cifras en base 10 presenta una distribución de primeros dígitos conforme a la Ley de Benford, al expresar esos mismos valores con otra base de numeración distinta las nuevas cifras que resulten de la nueva base también ajustarán las frecuencias de sus primeros dígitos a la bendita Ley. (Noten ustedes que las frecuencias que para cada dígito de 1 a 9 nos da la fórmula de Newcomb, las de la tabla, se refieren a cifras en base 10, por eso el logaritmo que aparece en la fórmula es el logaritmo decimal, log₁₀. Cuando se trate de cifras en otra base b cualquiera habrá que volver a calcular las frecuencias de los (b-1) dígitos con la misma fórmula, pero utilizando el logaritmo en base b, log_b. El gráfico de estas nuevas frecuencias tendrá distinto número de barras, (b-1), con otras alturas diferentes, pero imagino que dibujará una curva muy parecida, empezando por la más alta del 1 y acabando en la más baja del b-1).


Conclusión (provisional y abierta) y despedida (hasta enseguidita).

En fin, que hay desde 1938, al menos, un montón de gente aplicando la Ley de Benford a un montón de asuntos, descubriendo su vigencia en un montón de fenómenos y dándole a la famosa Distribución Logarítmica del Primer Dígito un montón de vueltas, todo lo cual resulta, como he tratado de contarles, sumamente instructivo y ameno, amén de sorprendente, al menos para mí. Pero lo que hasta ahora, en mi opinión, no ha hecho nadie, físico, matemático o filósofo, es explicar por qué existe y se cumple la propia Ley de Benford, por qué datos tan variopintos, obtenidos de fuentes tan diversas, desde las estrellas de las galaxias más lejanas hasta las del equipo local de fútbol, se obstinan universalmente en empezar por 1 y por 2 con una frecuencia mucho mayor que lo hacen por 8 y por 9, en qué se diferencian todos estos fenómenos, productores de datos benfordianos, del Bombo Universal de Lotería de que hablábamos en mi anterior post, que ignora olímpicamente a Benford, a Newcomb y a todos sus cálculos y produce en cambio números con una frecuencia de primeros dígitos escrupulosamente equitativa; y, más misterioso todavía, qué tienen en común entre sí todos estos fenómenos que distribuyen logarítmicamente los primeros dígitos de sus datos numéricos con arreglo a la misma pauta, siendo como son, en cualquier otro aspecto en que se los considere, cada uno de su padre y de su madre. Tras leer unos cincuenta o sesenta documentos abstrusos dedicados, en teoría, a responder estas preguntas, y tras dedicar otras cincuenta o sesenta horas a reflexionar yo mismo sobre ellas a la luz de lo leído, yo sigo estando igual de perplejo o más que estaba al principio.

Si Dios me da salud, dedicaré un tercer y último post a este asunto, en el que trataré de contarles, del modo más resumido, inteligible y ameno que me sea posible, estas reflexiones y perplejidades mías. La cosa promete ser verdaderamente dura. Ármense de amabilidad y de valor, y que Dios reparta suerte.


Estrambote teológico.

Entre las muy diversas aplicaciones de la Ley de Benford que he encontrado por Internet estos días de incesante investigación, hay una que no quiero dejar de consignar aquí, porque me ha resultado especialmente regocijante. Un tal Abdul Majis Motahari, que colabora en una página web cuya URL es esta significativa expresión: http://www.islam-soumission.org, dedica un apartado de dicha página, titulado "Milagro matemático" a contarnos, desbordante de éxtasis religioso, cómo la lista de 114 números que sale de contar cuántos versículos hay en cada una de las 114 suras del Corán se ajusta milagrosamente a la Ley de Benford. El articulo pueden leerlo ustedes aquí, pero para los que no tengan ganas o no se arreglen bien con el francés en que está escrito les resumo brevemente de qué va.

Resulta que según puede constatar cualquier lector del Corán que sepa contar, aunque Abdul lo constata cumplidamente para evitarle el trabajo, hay 30 suras con un número de versículos empezado por 1 (26'32 %), 17 suras cuyos números de versículos empiezan todos por 2 (14'92 %), 12 que tienen números empezados por 3 (10'53 %), 11 por 4 (9'65 %), 14 por 5 (12'28 %) , 7 por 6 (6'14 5), 8 por 7 (7'02 %), 10 por 8 (8'78 %) y 5 por 9 (4'39 %), lo cual es, efectivamente, una distribución que se aproxima muy razonablemente a la de Benford, sobre todo para tratarse de una muestra tan corta. No necesita más sidi Motahari para concluir la reconfortante evidencia: solo un texto dictado por Dios mismo podía cumplir en el siglo VII una ley que aún no había sido formulada. "Si Dios habla al hombre, sin duda utiliza el lenguaje de las matemáticas", nos recuerda el autor que dijo alguien tan poco sospechoso de ser musulmán como el matemático Poincaré.

El argumento de Motahari (aparte de que uno se pregunta por qué Alá no se ajustó más exactamente aún a la distribución de Benford, en vez de esta tímida aproximación, más propia de una lista de victorias madridistas entre 1911 y 1963 que de un Libro Santo), tiene varias consecuencias interesantes. En primer lugar, parece implicar que los datos, antes de que Newcomb y Benford les indicaran que debían hacerlo, no se atenían a la distribución logarítmica de sus primeros dígitos, salvo que mediaran expresas instrucciones divinas en ese sentido. Lo que no deja de ser una curiosa interpretación de las leyes empíricas que, según este buen imam, o lo que sea, no existen ni se cumplen hasta que alguien las descubre, Dios no mediante.

Y en segundo lugar, aplicando este criterio al Bhagavad Gita, al Quijote, a la Recherche du Temps Perdu o a la Guia Telefónica de Zaragoza, de todos los cuales textos podrá con toda probabilidad extraerse listas de números de palabras por capítulo o de letras por abonado que se ajusten igualmente a la Ley de Benford, debemos concluir que han sido, todos ellos, dictados por Dios en persona, no sabemos si por Alá mismo o por sus respectivas versiones locales.

Agradezco a Abdul Motahari este nuevo argumento que refuerza mi fe (lo malo es que igual ahora tengo que convertirme al Islam), y a mi corresponsal el conocimiento de este edificante artículo. Y nunca más escucharé sin protestar ese argumento según el cual el aumento de los conocimientos científicos irá poco a poco disolviendo las brumas supersticiosas de la religión. ¿Algún problema, digo, para conciliar a partir de ahora la ciencia con la fe?