PALABRAS PARA JOSÉ AGUSTÍN

Tengo que agradecerle a Goytisolo, entre otros, haber acabado por aceptar que nunca pude ser “de izquierdas”. Iba a añadir “Y eso que lo intenté…”, pero no, ni siquiera es así. No necesité intentarlo. En mi generación y en mi medio hacerse de izquierdas era un proceso natural, simultáneo, si no consustancial, con hacerse mayor. Uno crecía, intentaba enterarse de cómo era el mundo y de qué se podía hacer en él, y la respuesta que todo su entorno le ofrecía era, naturalmente, hacerse de izquierdas. Desde los padres -en mi caso la madre- de los que era necesario emanciparse y disentir, y que eran convencida y convenientemente franquistas, hasta los hermanos mayores, los amigos, los amigos mayores y los adultos cercanos cuyo ejemplo se proponía, que eran todos, en mayor o menor medida, antifranquistas y “progres”, -algunos, incluso, sospechosos de militar, lo que suponía el grado máximo de adultez, compromiso y vida verdadera-. Toda mi generación, al menos en mi medio, fuimos de izquierdas de un modo implícito, por defecto. Las escasas excepciones se consideraban fenómenos pintorescos, que mirábamos con cierta indulgencia burlona, sin polémica -innecesaria, puesto que era obvio que éramos nosotros los que teníamos razón-. Siempre hay un pelirrojo, un tartamudo, un filatélico o un facha para dar variedad al grupo. 

 

Coreé emocionado, por tanto, cada vez que había ocasión, uno de los numerosos “himnos” de la progresía española de los setenta: las “Palabras para Julia” de José Agustín Goytisolo, con la música solemne y salmódica que le puso Paco Ibáñez. Ya saben ustedes, esa que empieza: “Túu no pueeedes volver atráaas, porque la viida ya te empuuja, con un aulliido interminable, interminaable…” Y sigue así más rato. 

 

Pero incluso entonces, con todo mi fervor intacto, unos versos me chirriaban: “Un hombre solo, una mujer, así tomados de uno en uno, son como polvo, no son nada…” Los omití mentalmente. Preferí quedarme con lo de “nunca te entregues ni te apartes junto al camino, nunca digas no puedo más y aquí me quedo…”, “Otros esperan que resistas, que les ayude tu alegría…”, “La vida es bella, ya verás cómo a pesar de los pesares tendrás amigos, tendrás amor…” Pude así convencerme de que el poema era un canto a la vida, a la alegría, a la solidaridad y a la lucha -contra qué no era preciso especificarlo, era obvio, contra los malos…-, pude prescindir temporalmente del hombre solo que no es nada, considerándolo un residuo estalinista de los años duros en que fue escrito, y logré adscribir el conjunto así purgado al proyecto revolucionario y feliz de los nuestros, en el que un mundo nuevo y estupendo -que, naturalmente, no hacía falta decirlo, conservaría todos los rasgos confortables, amables y familiares del viejo-, iba a recolocarlo todo en un orden de cosas más justo y luminoso. Era evidente y facilísimo, Franco se iba a morir en breve, en afortunada coincidencia con nuestra entrada en la edad adulta, y el futuro no podía ser más prometedor ni más de izquierdas. 

 

Es curioso cómo una relectura de las famosas Palabras me deja ahora la impresión contraria, la de un desaliento, una resignación y una tristeza en las que los versos que omití pasan a ser el centro del poema, junto con estos otros que omitió Paco Ibáñez: “Por lo demás no hay elección, y este mundo tal como es será todo tu patrimonio”. El bueno de Ibáñez debió de darse cuenta de que su voz grave y vibrante, afirmando “por lo demás no hay elección…” no iba a quedar precisamente enardecedora, y decidió no incluir esta parte en su enardecedora canción. 

 

Por motivos no muy distintos pasé yo elegantemente por encima de “Un hombre solo, una mujer…”, pero el chirrido se me quedó ahí. Yo podía no tenerlos en cuenta, pero los versos estaban. Y cada vez me parecían menos un residuo omisible, y más el meollo del poema, el núcleo que irradiaba al resto su pesimismo, lo teñía de desesperación y lo convertía en un esfuerzo patético por transmitir alegría, hecho por alguien que carecía por completo de ella. 

 

 (Ha habido más canciones izquierdosas que me han ayudado a tomar distancia de la izquierda. Todavía con los rescoldos del primitivo ardor, aún convencido de ser un socialdemócrata de izquierdas con más simpatías hacia la Cuba de Castro que hacia los EEUU de Reagan, no podía evitar amargarle a mi amiga Merche, a quien Dios tendrá en su Gloria, esa estrofa de la Canción del Elegido, de Silvio Rodriguez, que dice “La última vez lo vi irse entre humo y metralla, contento y desnudo. Iba matando canallas con su cañón de futuro”. Cuando ella acababa de cantarlo, tan contenta, tan progre, tan enamorada de Silvio, yo le explicaba: “Llevaba al lado un comisario político que le iba señalando: ‘ese es canalla’, ‘ese no,’ para que supiera a quién matar…”  

 

En buena medida hablaban ahí mis permanentes ganas de llevar la contraria y mi incapacidad de dejar pasar la ocasión de hacer un chiste -y, todo hay que decirlo, mi tímido deseo de explorar, por retorcidos caminos, las posibilidades de ligar con Merche, porque me encantaba que ella me contestara “¡Ay, qué idiota eres!”, y me diera un cariñoso manotazo-. Pero hablaba, también, esa parte de mí que ya entonces se negaba a aceptar que un hombre solo, una mujer, así, tomados de uno en uno, sean como polvo, no sean nada, y puedan, en consecuencia, ser alegremente barridos como canalla por el cañón de futuro del amigo Silvio). 

 

“Con los comunistas hasta la muerte, pero ni un paso más allá”, parece que dijo un ingenioso e insigne hijo de puta que, por cierto, cumplió fielmente su aforismo durante toda su vida, y acompañó de variadas maneras a los comunistas hasta la muerte. Hasta la muerte de otros, claro. Los acompañaba en el Madrid de 1936, cuando escribía “A paseo” para señalar justicieramente a quién debían asesinar a la siguiente madrugada, y los siguió acompañando en sus últimos años, cuando, en su retiro del País Vasco, le hacía los coros en bonitos sonetos -escribía bien, el cabrón, y no versificaba mal- a los asesinos de ETA. Dios, que es infinitamente misericordioso, se lo habrá perdonado, así que poco puede perjudicarle el asco profundo que siempre me ha inspirado el sujeto. 

 

Pero no sé a qué ha venido la irrupción en mi sesudo escrito de semejante individuo… 

 

Ah, sí. La gracieta de Bergamín, si impedimos, esforzándonos un poco, que su significado se deslice naturalmente al que acabo de darle yo, y lo mantenemos ortodoxamente en el que le dio su autor, es de una profunda necedad, pero en su día a mí me pareció una buena fórmula para describir mi propia postura. Porque yo era de izquierdas, sí, por necesidad histórico-sociológica, pero era también creyente, primero por parecidos motivos pero enseguida, ya desde temprana edad, por elección personal y convicción profunda. Y por cierto que realicé durante bastantes años y con una facilidad sorprendente -producto de la nula exigencia del público benevolente, yo incluído, que andaba a otras cosas,- los malabarismos necesarios para mantener al mismo tiempo ambas profesiones de fe fingiendo creer que eran compatibles, malabarismos para los que la frasecita venía muy bien. Como yo no asesinaba, ni mandaba asesinar, ni aplaudía a los asesinos, ni creía, en general, -pobre ingenuo- que la cuestión de matar gente fuera consustancial a la revolución y al progresismo, me resultó más fácil que a Bergamín. La muerte, en mi caso, era una cosa ajena y lejana. Pero, aún así, la conciliación tenía sus dificultades. Para mí, solo teóricas, afortunadamente. Pero dificultades. 

 

La dificultad fundamental no estaba explícita, porque habría desbaratado toda la construcción, pero, oculta y todo, no podía estar más clara: no se puede estar al mismo tiempo con quien cree que un hombre solo es como polvo, no es nada; con quien fía toda la felicidad que la pobre Julia va a encontrar en este único mundo al problemático calorcillo que puedan proporcionarle la amistad y el amor de otros cuantos millones de resistentes a pesar de los pesares, tan desesperados como ella y como su padre… no se puede estar con esa gente, digo, al mismo tiempo que con quien afirma que una sola vida humana es infinitamente valiosa, y promete a cada individuo una felicidad eterna. La boutade de Bergamín, neciamente ingeniosa, envuelve esta imposibilidad y finge así superarla, pero el caso es que, en contra de lo que afirma, la incompatibilidad radical entre ambas creencias no aparece solo un paso más allá de la propia muerte. Empieza a manifestarse como evidente bastante más acá. Díganlo si no él mismo y sus envíos a paseo. 

 

A mí, concretamente, la dificultad se me planteaba, insidiosamente disfrazada de ser otra cuestión y permitiéndome así creer que no me afectaba, cada vez, por ejemplo, que escuchaba una exhortación a la unión que hace la fuerza. Lo utilice quien lo utilice, desde pequeño me ha irritado mucho ese mecanismo por el que basta invocar la necesidad de marchar todos unidos para que la cuestión de hacia dónde pase a una discreta segunda fase de la que no se habla más que vagamente. “La unión hace la fuerza”, dicen unos y otros, porque en eso todos están de acuerdo: unidad de la clase obrera, unidad de los buenos patriotas, unidad contra el terrorismo, unidad de los funcionarios de administración local con habilitación de carácter nacional… Y a mí, que desde mis cuatro años he necesitado orden y método para no perderme en mis trabajosos procesos mentales, lo primero que se me ocurre es preguntar: ¿La fuerza para hacer qué? Porque antes de unirme, me gustaría saberlo… 

 

Pero preguntar eso, amigo, es ya ser un cochino disidente, uno de esos individuos problemáticos que impiden la unión que hace la fuerza. Uno de esos tipos asociales que se niegan a admitir que un hombre solo, una mujer, así, tomados de uno en uno, son como polvo, no son nada… ¡Fuego en ellos! Marcha con el pelotón, desgraciao, y no preguntes tonterías. 

 

Yo, lo siento, no puedo. Ni quiero. Tras el indiscutible imperativo de “unidad”, que a todos parece obvio, a mí siempre me resuenan insidiosamente los versos de Goytisolo que tanto empeño puse en su día en esquivar y, a continuación, mi inevitable corolario: Su puta madre, no será nada. Yo soy yo, y antes que hacerme fuerte uniéndome quiero saber a quién, por qué razones, con qué objetivos y con qué medios. Porque es que lo mismo no me gustan las respuestas, y no me quiero unir… 

 

Y si eso te pasa no puedes ser de izquierdas. Para la izquierda tú, un hombre solo, o una mujer, así, tomado de uno en uno, eres como polvo, no eres nada. Y eres, por ello, candidato perfectamente elegible para asesinar o ser asesinado, y Bergamín te mandaría a dar el paseo a alguien, o a que alguien te lo diera a ti, sin el menor problema, porque no debe haberlo en quitar de en medio a un poco de… nada… que obstruye la marcha imparable -no preguntes hacia dónde, mota de polvo- de la unión, que hace la fuerza. 

 

Si no crees ser como polvo, si no crees no ser nada; si crees ser alguien, merecer algo por ti mismo, ser el dueño y el responsable último de tus actos y tener el derecho, y el deber, de escoger por ti mismo tus objetivos y tus caminos; si crees que cada único ser humano tiene un valor infinito y que nada puede justificar su asesinato; y, si, en consecuencia, crees que unirse para ser fuertes no es un imperativo categórico, y que, antes de hacerlo, quieres elegir a quién te unes, para marchar hacia dónde, a hacer qué, con qué maneras… entonces no puedes ser de izquierdas. 

 

No puedo ser de izquierdas. Nunca, en realidad, he sido de izquierdas. Me ha llevado años comprenderlo, aceptarlo y, finalmente, congratularme por ello. Y en este proceso José Agustín Goytisolo y sus Palabras para Julia me han resultado, ya ven ustedes, francamente iluminadores. No es pequeño servicio. Les quedo considerablemente agradecido.

Karaoke a través del tiempo

 
Mi madre - Caminito. Con mi acompañamiento al piano, cuarenta años después, hecho con FinaleNotepad 
 

Mi madre cantaba. Casi todo el rato que no estuviera haciendo algo que se lo impidiera. Cantaba con buen oído y bonita voz, además, y tenía un repertorio impresionante de canciones, aprendidas desde su infancia, primero de la muchacha que trabajaba en su casa, que debía de ser también una cantarina de buen oído -disculpen la terminología rancia y clasista, la muchacha era una institución rancia y clasista y no conozco para ella un término mejor- y luego de la radio y hasta del cine.

Así que una tarde de hará quizás cuarenta años, sola en casa y presumiblemente aburrida, cogió una cassette y se grabó a sí misma, cantando a capella todas las canciones que se le fueron ocurriendo. Entre quince y veinte canciones, una buena hora de grabación. Una cinta de sesenta minutos, que fue luego a mezclarse con las otras cien o doscientas que andaban por mi casa con toda clase de música, en aquellos tiempos en que grabar de un disco prestado la música que nos apetecía era el único modo de procurárnosla quienes que no teníamos dinero para comprar nuestros propios discos. Y allí se quedó, y alguna vez la oiríamos, supongo.

Hace treinta años que murió mi madre. Poco después vaciamos la casa, y el montón de cassettes, ya prácticamente inservibles, se vino para la mía. Algunas músicas que me interesaban especialmente y no veía fácil conseguir de otro modo fui poco a poco pasando a mp3, para almacenarlas en el disco duro de mi ordenador, donde guardo, como un obseso, cerca de 800 horas de toda la música que me gusta. (Ya sé que es un almacenamiento perfectamente inútil en estos tiempos de Spotify y música on line, pero yo soy antiguo, y no me parece que realmente tenga la música que quiero tener si no está guardada en mi ordenador, en mi Ipod y, por si acaso, en un disco duro externo). 

El caso es que en el proceso me topé con la cinta de mi madre. Es una sensación extraña, que no gusta a todo el mundo, la de oír la voz de una persona amada que ya ha muerto. A mí me emocionó y me encantó. Emepetreseé convenientemente todas las canciones y las uní a mi colección, como un tesoro especialmente valioso.

Pero no eran fáciles de oír. Aparte de las emociones encontradas, la voz a palo seco, sin acompañamiento y con las licencias rítmicas que mi madre se permitía, resultaba un tanto desabrida, y la audición me dejaba siempre un regusto raro, entre nostálgico y desolado.

Por aquel entonces descubrí el Finale Notepad, maravilloso programa que te permite escribir en el ordenador música que luego el propio ordenador hace sonar. Hice con él algunas chapuzas que me divirtieron enormemente y que quizás recuerden los lectores de este blog, si alguno queda a estas alturas, porque andan por aquí, colgadas en unos posts u otros. (Acabo de descubrir el modo de resucitar las músicas colgadas en el blog, que creía ya perdidas; es uno de los motivos por los que me he resuelto a volver a publicar algo aquí, ocho años después del último post).

Y un buen día me embarqué en el más difícil todavía de ponerle acompañamiento con el Finale a alguna de las canciones de mi madre. Hasta entonces el proceso había sido el de escribir primero la parte del piano y acoplar luego mi voz a él, pero esta vez había que hacerlo al contrario: escribir un acompañamiento que se adaptara a una voz ya existente. No estaba nada seguro de conseguirlo, pero me apetecía mucho intentarlo.

La verdad es que solo lo conseguí con un par de ellas. La que encabeza este post, el tango Caminito, y esta otra, Deja que salga la luna, que a ella le gustaba especialmente, y que a mí me sigue emocionando cada vez que la oigo. Las demás tenían ritmos demasiado complicados, o demasiadas alteraciones caprichosas del tempo por parte de la intérprete, como para poder compaginarlas medianamente con la rigidez maquinal del Finale que, al fin y al cabo, no es un pianista de verdad (como yo mismo, por otra parte, que no lo soy ni de verdad ni de mentira). No pierdo la esperanza de lograrlo con alguna otra, cuando tenga tiempo, pero de momento estas dos son todo lo que hay.

 
Mi madre - Deja que salga la luna. Con mi acompañamiento al piano, cuarenta años después, hecho con FinaleNotepad 

Nunca hubo manera de acompañar el canto de mi madre en directo. Tenía su propio sentido del ritmo, y al acompañante le costaba sudores seguirla. En una casa en la que cualquiera se ponía a cantar en cualquier momento, y enseguida salía una guitarra, -y a veces hasta un piano aporreado- para acompañarlo, y un par de voluntarios para los coros, mi madre se unió rara vez al barullo general. Era vocacionalmente solista, y yo me quedé con la pena de no haber hecho casi nunca música con ella.

Con estas dos canciones me he resarcido. Renuncio a explicar la profunda satisfacción que me produce oír a mi madre y a mí haciendo música juntos, aunque sea con cuarenta años de distancia entre su aportación y la mía.

Confesión inopinada y ligeramente bochornosa con ocasión del día de San Jorge

Siempre es tiempo para corregir una omisión: aunque tarde, este post va dedicado a Cigarra –que es, por cierto, un nom de guerre scout–, con mi agradecimiento. Nadie lo merece más, y pocos lo entenderán igual de bien. 

Aunque son muchas las cosas que me gustan de los ingleses y soy, en conjunto, bastante más anglófilo que lo contrario, soy también consciente de muchas características británicas más bien desagradables. Entre ellas, señaladamente, el desparpajo con el que se han venido adueñando, de tres o cuatro siglos a esta parte, de cosas que originalmente no les pertenecían: el té, por ejemplo, las Indias (la fetén, la oriental, y las occidentales de México para arriba), la institución del mayordomo, Irlanda del Norte, el friso del Partenón, la Promenade des Anglais de Niza, buena parte de las Islas Baleares, la segunda lengua de todo quisque (y la primera de unos cuantos), el Peñón, la costumbre de carraspear antes de hablar... La lista de sus predaciones es interminable, e incluye hasta un santo, que es a lo que hoy quería yo ir. 

San Jorge es un santo de existencia problemática. Apenas sabemos nada cierto de él salvo que con toda probabilidad no fué inglés ni cosa que se le parezca, sino capadocio –turco, mayormente–. Como es un santo gallardo y vistoso son muchos los lugares que lo han nombrado su patrón, además de Inglaterra: Aragón, Barcelona, Portugal, Lituania, Georgia, Cáceres y Moscú, sin ir más lejos. Pero los ingleses se lo han apropiado con especial empeño y lo han convertido en un gentleman rural británico, con safari en tierras exóticas incluido (el dragón); y los demás hemos aceptado esta ocupación tan dócilmente como la de Gibraltar. Es una habilidad que tienen para hacer pasar su predominio por una amable tradición más, a la que no solo es fácil acostumbrarse sino que no hacerlo parecería como de mala educación... 

A pesar de esta apropiación indebida de que ha sido objeto por parte de los ingleses –o quizás a causa de ella, al menos en parte– San Jorge es para mí un santo especialmente simpático, como he contado en otra parte, y creo que esta simpatía se debe, al menos en su origen, al hecho de que sea, además, el patrón de los boy scouts, hueste en la que milité en mis años mozos. 

Sí señores, he sido boy scout, y he sido muy feliz siéndolo. En las dos variedades sucesivas que, tan exacta como rudamente, retrata esa famosa definición de «unos niños vestidos de gilipollas mandados por un gilipollas vestido de niño». Fui niño vestido de gilipollas y, a su debido tiempo, fuí también gilipollas vestido de niño, si bien solo en el orden simbólico o metafísico, porque en la práctica mis scouts eran poco adictos a los uniformes y más bien íbamos todos, niños y menos niños, vestidos de guarros. Asumo todos los inevitables chistes, incluyendo el realmente bueno de la definición, los comprendo y entiendo incluso a quienes desconfían del tufillo militarista, autoritario y rancio que, visto de lejos –y, en algunos, pocos, casos, de no tan lejos– presenta este benemérito movimiento. Hasta entiendo a los que se irritan cuando se encuentran en el campo con una de estas manadillas infantiles, porque a mí me pasa lo mismo, detesto irracionalmente encontrar gente donde igual de irracionalmente creo que solo yo debo estar. Pero tras entenderlo todo, no tengo más remedio que proclamar que fui muy feliz siendo scout, que serlo tiene en mi vida una influencia tan importante como beneficiosa y que, en resumen, creo deber a mi scoutez (escultismo es la palabra técnica) buena parte de mi capacidad de ser feliz, no solo la de entonces sino también la de ahora mismo. 

Nunca aprendí en los scouts esas cosas que la mitología popular afirma que enseñan: hacer nudos, orientarse en el bosque o encender un fuego frotando dos palitos. Mis scouts debían de pertenecer a una variedad más intelectual y metafísica, y descuidaron el cultivo de estas apreciables habilidades, aunque felizmente no faltaron las acampadas y las marchas. Pero en cambio aprendí con ellos otras cosas que juzgo más importantes y útiles, tanto que aunque de mis tiempos de escultismo activo hace casi cuarenta años, y los detalles y las anécdotas están prácticamente borrados de mi mala memoria, esas cosas que digo me han acompañado desde entonces y han crecido conmigo, porque tenían la importancia y la consistencia suficientes como para ser igual de válidas a los quince años que a los cincuenta.

Hablo de cosas muy elementa­les, muy concretas, pero de mucha importancia práctica y vital. Cosas que han modelado muy significativamente las actitudes y los comportamientos frente a la vida que todavía ahora sigo intentando, con éxito desigual, que sean los míos. Experiencias y aprendizajes que tienen que ver con la manera de habitar el mundo, intentando, al mismo tiempo, entenderlo, disfrutarlo y mejorarlo; con la disposición hacia los demás, desde un sincero deseo de servicio hasta una actitud de respeto, acogida y cordialidad;  y con el modo de convivir con uno mismo, firmemente asentado en la confianza, humilde y realista, pero optimista y tenaz, en las propias capacidades. 

Y tienen sobre todo que ver, como les decía hace un par de párrafos, con mi capacidad de ser feliz. Quizá el concepto de felicidad no sea un criterio muy sólido ni respetable, y quizás por ello esta afirma­ción suene un tanto frívola y evanescente en algunos oídos, pero no, desde luego, en los míos. Creo firmemente que en la vida se pueden hacer pocas cosas más difíciles ni más importantes que aprender a ser feliz. 

Mi idea de la felicidad, lo que hoy experimento cuando me siento plenamente feliz, es exactamente lo que experimentaba a los quince y a los veinte años, en medio de un campamento o una salida con los scouts. Quien lo ha vivido sabe que no hay felicidad igual a la del día que te montas en el autobús o en el tren con tu tropa para empezar un campamento –que, en tu ánimo, es todo el futuro que existe, porque los campamentos, como las vacaciones, son eternos, y ni se anticipa su final ni merece la pena perder el tiempo en pensar en lo que vendrá después–, con una gente que, en tu cabeza, es toda la gente que hay en el mundo –quieres mucho a tu familia y ella te quiere mucho a ti, pero, precisamente por ello, puedes borrarla totalmente de tu mente durante veinte días con toda tranquilidad–; y que todas las felicidades que se experimentan después tienen a aquella por patrona y fundadora. No hay relación con el mundo que pueda compararse a la que sientes en las tripas cuando sales de la tienda en medio del monte con un frío pelón; y el aire helado de la mañana, el cielo, el paisaje y tus amigos son lo más real y lo más tuyo que has tenido nunca, y el nuevo día se presenta ante ti como una aventura invitadora, deslumbrante y feliz.  Si has tenido la suerte de vivir esas cosas a los diez y a los quince años, ya sabes qué es lo que te interesa en la vida, y a partir de ellas modelas todo lo que viene después. Todo lo que más tarde puedas hacer se basa en aquello. Todas mis actividades de adulto, toda mi vida, no tratan de ser, en el fondo, más que un desarrollo puesto al día de aquellas felices experiencias de niño y de adolescente, y creo que son esa disposición que en mi inconsciente la preside, y esa intención, más o menos expresa y que nunca me abandona del todo, de no defraudar al chaval idealista que sigue mirándome, expectante, desde algún pinar, las que hacen que la disfrute tanto.

Y no sé si consecuencia o causa de lo anterior, pero fundamental en todo caso: aunque por lo que yo recuerdo nuestras actividades scouts no eran especialmente «piadosas», ni había en ellas gran cosa de religiosidad explícita, lo cierto es que el Dios en que actual­mente creo es el mismo en que aprendí a creer entonces, que la relación que mantengo con Él es la misma que entonces empecé a establecer y a afianzar y que la clase de vida que trato de vivir es la que entonces descubrí que quería intentar que fuera la mía. Creo que si hoy sigo siendo creyente se debe, en buena medida, al modo en que en aquellos años aprendí a plantear y a vivir mi fe, bajo la influencia, no única, pero sí muy importante, del escultismo. Sigo sin tener mejor idea de la vida eterna que «la paz de un eterno campamento» de la que habla la vieja canción scout. Si solo le debiera eso al escultismo, ya creería deberle más de lo que nunca le podré pagar. 

Debo precisar, por último, que mis boy scouts tenían con el ilustre imperialista inglés que fundó el movimiento, y con sus prácticas campestres y paramilitares, bastante poca relación, y esa poca más simbólica que otra cosa, más afectiva que efectiva. Suele pasar con las instituciones que crecen y se desarrollan por caminos en gran medida insospechados para su fundador, y el escultismo católico español de los años setenta le habría resultado al coronel Baden Powell, me temo, no solo irreconocible, sino bastante ajeno y poco apetecible. Tanto como él, su bigote, sus insignias, su uniforme militar y su sombrero de cuatro bollos nos lo habrían resultado a nosotros. Felizmente, para el uno y para los otros. Cada cual tiene su camino y sus maneras. 

Lo cual no me impide agradecerle en el alma la fundación del escultismo y desearle a su espíritu inmortal, a los scouts del mundo y a todos ustedes un feliz día de San Jorge.

La vida misma

Escenas de la vida real (unas más que otras)

1.- Los ferreteros son una casta intimidante. Aprendí a lidiar con ellos a los diez años, una vez que quise comprar unos tornillos para algún trabajo manual que por entonces ocupaba mis ocios. Examiné un poco abrumado las diez o doce muestras de tornillos que el demiurgo había extendido displicentemente sobre el mostrador de madera, escogí uno que me pareció adecuado y pregunté tímidamente: «¿Cuánto es la docena?» «Doce», me respondió, ingeniosísimo. Yo echaba cuentas, desesperadamente, y como no me parecía posible que una docena de tornillos costara semejante disparate de dinero, insistí: «¿Doce?» «Sí, sí, la docena son doce», remachó él, en el colmo del regocijo, y entonces caí. Me enfadó tanto su estúpido intento de reirse de mi timidez que saqué fuerzas para seguir adelante y comprar los tornillos, y desde entonces nunca me acerco a un mostrador de ferretería sin el ánimo dispuesto para la pelea. 

Un buen recurso es alardear de entrada de la propia ignorancia, exhibiéndola como una ventaja nuestra sobre su despreciable erudición. «Al fin y al cabo», se trata de que diga nuestra actitud, «tú eres el que no tiene más remedio que entender de estas cuestiones menestrales y menores. Demasiado hago yo, normalmente ocupado en más altos quehaceres, al interesarme momentáneamente por esta tu minúscula e irrelevante parcela del conocimiento».

No siempre funciona, pero ayuda a abandonar el local con cierta dignidad. 

2.- Un atardecer de abril de hace años, sentados en una terraza de una calle romana, A, una novia mía de entonces, y yo mirábamos el mundo. En una mesa cercana se sentaba, solo, un hombre de treinta y tantos o cuarenta años, elegante y bastante guapo. Yo no ví en él nada de particular, esa arrogancia masculina de los italianos que se saben guapos, si acaso. A, después de mirarle un momento en silencio, se estremeció, me agarró del brazo y me rogó con lo que me pareció verdadera angustia que nos volviéramos al hotel. No quiso explicarme nada hasta que no estuvimos lejos, y aun entonces solo me dijo que aquel hombre era «malo». «¿Pero es que lo conoces?» «No lo había visto en mi vida hasta esta tarde». «¿Pero te ha dicho algo, te ha hecho algo?» «No me ha hecho ni dicho nada, apenas me ha mirado. Pero es malo, lo noto. Es peor que malo, es... el mal». Es todo lo que fue capaz de explicarme, pero estaba verdaderamente afectada por la breve visión de aquel buen señor en el que yo apenas me fijé. Pasó los siguientes días inquieta, no acabó de disfrutar Roma, todo el tiempo parecía estar asegurándose de que no había nada malo alrededor. No volvimos a verlo y al poco nos fuimos de Roma. A no volvió a hablar nunca de aquella tarde, y cambiaba rápidamente de tema las pocas veces en que yo aludí a ella. 

(A no usaba relojes porque los estropeaba; enloquecía el cuentarrevoluciones de su coche hasta que renunció a seguir llevándolo a arreglar, y quitaba a sus amigas el dolor de cabeza colocándoles las manos encima. Era agnóstica, psicóloga e incapaz de entender el problema más elemental de la persona más diáfana que tuviera al lado sin complicarlo hasta la ininteligibilidad con alguna teoría mal aplicada de algún manual de su Facultad...) 

3.- En una tienda de una ciudad manchega asistí a una escena muy edificante. Un cliente se sentía estafado y discutía acaloradamente con la dueña, una gorda plácida que escuchaba impertérrita las quejas y los argumentos. El hombre quería, con razón por lo que pude enterarme, que le devolvieran su dinero, y la tendera, sin perder la calma, se negaba en redondo. La cuestión se fue agriando y el cliente, cada vez más frustrado, pasó a los insultos. La llamó ladrona, estafadora, sinvergüenza y choriza sin que a ella le cambiara el gesto, ni respondiera más que con fórmulas corteses, ni dejara de sonreir ni, por supuesto, devolviera una sola peseta. Pero cuando, exasperado, se le ocurrió llamarla gorda... entonces ella se descompuso, salió de detrás de su mostrador clamando que qué se había creído y le echó de la tienda sin más contemplaciones. Era gorda, evidentemente, y me dio toda la impresión de que también un poco ladrona, sinvergüenza y estafadora. Sin embargo que le llamaran esto último no le importaba, debía de considerarlo una opinión discutible pero respetable. En cambio lo de gorda, que era un hecho obvio e incuestionable, no fue capaz de encajarlo con la misma paz.

 
Georges Brassens - Tonton Nestor. Versión libre en español de Júbilo Matinal (Tío Pascual)

(Para estudiar la excelente versión española con más detalle, pinchar aquí)

4.- Es conocido, o debería serlo, el dato verídico –inventado por mí mismo hace solo un rato, de hecho– de que los churros de la madrileña chocolatería de San Ginés los hacen en un polígono industrial del valle del Yang Tse. El mismo en el que precocinan la butifarra amb mongetes que se sirve en la mitad de los bares de carretera de Cataluña. Concretamente en una fábrica que montó hace ya años, con una subvención de Asuntos Exteriores para la expansión empresarial española, un industrial de Mataró. Un ciudadano ejemplar, de la ejecutiva provincial de Convergència, aunque hace años que vota en secreto a Esquerra, porque, cuando su primogénito estuvo a punto de afiliarse al PP, él le prometió a la Moreneta hacerlo así si curaba el españolismo de su pobre hijo. La Virgen atendió su ruego, él dedicó devotamente su voto a los republicanos y el muchacho se fue a vivir a Rentería y se hizo nacionalista vasco. Hasta lo detuvieron en Hendaya una vez, por seguir a un empresario francés, precisamente el socio de su padre en la fábrica china. El francés se molestó un poco, pero el padre andaba muy orgulloso de la iniciativa de que daba muestras su chaval. 

Como suele ocurrir con los milagros realmente útiles, la intervención mariana tuvo lugar a través de mediaciones puramente humanas, concretamente del Servicio de Salud Vasco, Osakidetza o algo así, creo que se llama. Sucedió de este modo: su padre lo matriculó en Deusto, para alejarlo de la pija rubia del PP que le traía a mal traer. El cambio de clima, la abstinencia sexual, el chiquiteo y la poca costumbre de estudiar le provocaron tremendos dolores de cabeza, y acudió a Urgencias (Larrialdiak, para ser exactos), en donde se produjo una pequeña confusión: le desviaron por error al Programa de Normalización de Tallas de Txapelas y allí, en cumplimiento del protocolo previsto a tan eusquérica finalidad, le extirparon el lóbulo frontal del cerebro, la parte de la corteza cerebral donde radican la empatía y el pensamiento abstracto; perfectamente superflua, vamos. Tras cuya operación dejó los estudios, se mudó a Guipúzcoa y entró en contacto con unos abertzales muy simpáticos, que dieron un nuevo sentido a su vida. 

Como él mismo decía a quien le quería oir: los caminos del Señor, oyes, que son muy suyos, joder, me cago en la hostia, pues. (Porque desde que Nuestra Señora le volvió al buen camino se hizo bastante meapilas, también).

La jornada de un obseso mental. Y Parte 3ª

Para Ricardo, por proveerme de combustible. Y para Miroslav, por prestar atención a mis humaredas y hasta dedicarles un post.

Recuerden ustedes que este post es el tercero de una serie con primera y  segunda parte, que espero que lo hagan un poco más inteligible.


La convalecencia.

Quedamos en que yo estaba hondamente perturbado por los inesperados sucesos que habían tenido lugar en mi ordenador.

Eran mis datos, obtenidos a golpe de mi dedo, con mi simulador, los que desafiaban impertinentemente leyes fundamentales de la estadística, bajando y subiendo irresponsablemente en circunstancias en las que habrían tenido que limitarse a bajar.

Era en mi tabla de frecuencias donde una clínica de diez nacimientos diarios se permitía alcanzar o superar el sesenta por ciento de varones más frecuentemente que otra de solo cuatro nacimientos diarios, en abierta rebeldía contra el principio indiscutible según el cual debía hacerlo menos frecuentemente.

Urgía encontrar una explicación a acontecimientos tan escandalosos. Y sobre todo urgía tomar la primera medida que a uno se le ocurre en situaciones como esta: buscar alguien a quien echarle la culpa.

Yo empezaba a barruntar una posible explicación de la sorprendente conducta de mis frecuencias, pero no iba a ponerme a investigarla sin estar seguro de que la cosa lo mereciese. Ganas de perder el tiempo y de buscarse problemas sin necesidad.

No, no; lo conveniente era que, antes de que yo me enredara en explicaciones comprometedoras, alguna autoridad matemática competente se hiciera cargo de la peligrosa situación, asumiera la responsabilidad de lo que allí estaba pasando y estableciera oficialmente si aquellas cifras mías podían o no dedicarse legítimamente a pegar saltos.

De modo que me puse a buscar con denuedo a esa autoridad matemática. En Internet, claro, dónde si no. Mis Matemáticas de COU, última ocasión en que yo supe algo de Cálculo de Probabilidades, yacían perdidas por algún rincón poco frecuentado de mi memoria, y a quitarles el polvo con la ayuda de Gúguel me apliqué con ahínco.

Afortunadamente tardé muy poco en dar con Daniel Bernouilli, un señor del siglo XVIII, medio holandés, medio suizo, que parecía dispuesto a interesarse por mi problema. A mí me sonaba que era físico y se ocupaba de cosas como cañerías y fluidos, pero por lo visto también se había interesado por las probabilidades. Con los sabios del XVIII y del XIX da gusto, servían para un fregado lo mismo que para un barrido, sabían de todo. No como los de ahora, que en cuanto nos sacan de nuestra especialidad ya no sabemos ni por dónde nos andamos.

Este buen señor, me informó la Wiki, habia estudiado largamente, e incluso dado nombre, a la distribución de variable discreta de Bernouilli.

Lo de "discreta" empezó ya por caerme en gracia: si había yo metido la pata con mis exceles, no quería darle tres cuartos al pregonero y que se tuviera que enterar todo el mundo.

Hablando más propiamente, precisamente por ahí iban mis esperanzas de explicación: los altibajos de mis datos se producen, empezaba yo a creer, porque se refieren a un fenómeno discreto, y no continuo. Esto es, porque su variable (el niño o la niña) no es infinitamente divisible, sino que tiene una unidad mínima, indivisible: el bebé propiamente dicho, que no puede ser dividido sin provocar comentarios. Ese de la discreción creía yo que iba a resultar el quid del asunto –luego hablaremos de ello, no se preocupen–, y por eso la distribución esta de probabilidades, sea lo que fuere, con ese nombre tan oportuno, tenía toda la pinta de venirme al pelo.

Y así resultó ser porque, según la Wiki, Don Daniel sabía cómo se calcula lo que precisamente necesitaba yo averiguar por vías distintas de las empíricas que tantos problemas me estaban dando: cuál es la probabilidad de que, de diez niños nacidos, seis sean varones.

Él, más genéricamente, enfocaba el asunto así: la probabilidad P de que al realizar n veces un ensayo se produzca k veces uno de los posibles resultados (cuya probabilidad individual es p) viene dada por la siguiente fórmula:

Que se vuelve menos hermética si recordamos que n!, "ene factorial", es el producto de todos los enteros desde 1 hasta n. Y más legible todavía si, aprovechando que nuestro caso no presenta más que dos posibles resultados, niño o niña, cada uno de ellos con una probabilidad de 0'5, por lo que p y (1-p) valen ambas 0'5, la escribimos así:

Con lo que ya estamos en condiciones de cambiar n por 10, y k por 6, y encontrar que la probabilidad de que haya seis niños entre diez recién nacidos es:

Lo que, realizadas las operaciones correspondientes, resulta valer 0'20507

Pero no solo nos sirve alcanzar el 60% de niños, los 6 calculados; también nos vale superarlo. O sea, que también tenemos que considerar como resultado favorable que nazcan 7, 8, 9 o 10 varones. Y podemos calcuar igualmente las probabilidades de cada uno de estos casos:

De que haya siete niños  : 0'11719
De que haya ocho niños  : 0'04394
De que haya nueve niños: 0'00976
De que haya diez niños   : 0'00098

Sumando estas cinco probabilidades obtenemos la de alcanzar o superar el 60% de varones con diez nacimientos diarios: 0'37695.  El 37'7% de probabilidad.

(Mi simulador decía que era el 37'5%, dos décimas menos. No iba tan descaminado).

Si hacemos lo propio con la clínica de cuatro nacimientos diarios, que supera el 60% de varones cuando nacen 3 niños (75%) y cuando nacen 4 niños (100%), nos encontramos con que en su caso las probabilidades son:

De que haya tres niños     : 0'25000
De que haya cuatro niños: 0'06250

Que suman 0'31250, un 31'25% de probabilidad. Mi hoja de Excel la había fijado en el 31'0%. Otra vez dos décimas menos. Se desvía hacia abajo, parece, tendré que ajustarle la mira. 

Bueno, pues asunto aclarado. Qué fáciles se vuelven las cosas cuando las coge entre manos un experto. Ya podía yo descansar tranquilo. Mis frecuencias hacían cosas raras y con pinta de ilegales, sí, pero quedaba comprobado que las hacían con conocimiento y permiso de un matemático competente de reconocido prestigio. No era culpa mía, ni de mi simulador. De ser culpa de alguien, sería del Bernuiyí este, que para eso viene en la Wiki.

Mi satisfacción no se debía solo a haberme quitado ese peso de encima. Estaba también muy contento porque mis hojas de cálculo, a fin de cuentas, funcionaban bien. Ahora que conocía el modo de calcular las probabilidades teóricas, me apañé una nueva hoja con la formulita del holandés-suizo, con la que averigüé las frecuencias con que, según él, superaban el 60% de varones todos los hospitales de mi tabla. (Es decir, no todos, solo los 170 primeros. Porque para calcularlas hay que encontrar primero cuánto vale el factorial de su número de nacimientos. Ese "!" puesto detrás del numerito, ¿se acuerdan? que quiere decir que hay que multiplicarlo por todos los inferiores hasta el 1. Y Excel no da para calcular el factorial de números más grandes que 170. Habida cuenta de que el factorial de 170 vale 7'257 multiplicado por un 1 seguido de trescientos seis 0, tampoco es de extrañar).

El caso es que de las ciento setenta, más de la mitad coincidían exactamente (vamos, hasta el primer decimal, que es donde yo redondeé) con las que había encontrado yo a golpe de simular años dando clics en el ratón. Y, de la mitad que no coincidían, solo una se alejaba cuatro décimas (la del hospital de 5 nacimientos, un 50'4% que desde el principio me cantó), las demás se iban una, dos o, como mucho tres décimas arriba o abajo. No hacía falta ajustarle la mira, mira qué bien.

Y también estaba muy contento por haber puesto al día mis conocimientos de cálculo de probabilidades, que me vendrán muy bien para cuando juego al póker. Para perder con más conocimiento de causa.

Pero sobre todo estaba contento porque, por fin, había dado con la explicación de la conducta ciclotímica de las dichosas frecuencias. No hay como las matemáticas para poner las cosas en claro. Los altibajos de mi tabla tenían sus motivos, como enseguida veremos. De hecho solo parecían contradecir las leyes estadísticas, porque lo que en realidad hacían cuando pegaban esos botes tan espectaculares era cumplirlas escrupulosamente.

(Vaya, hombre, ahora que había quedado claro que no era culpa mía, resulta que todo está en orden y que no hay nada de lo que echarle la culpa a nadie. Siempre pasa lo mismo).

Y en realidad esta explicación, como todas una vez se conocen, era bastante simple. Se la cuento en cuatro párrafos:

Quizás recuerden uno de los dibujitos decorativos pero innecesarios de mi anterior post, en el que se señalaban, como por pasar el rato, los máximos y los mínimos locales de la quebradiza curva de frecuencias. Bien, a lo mejor no es un gráfico tan inútil como yo creía.

No se ve muy bien, porque Excel coloca las cifras de los ejes de aquella manera: pero las barras azules de este gráfico, que son los máximos locales de frecuencia, resultan todas corresponder a los hospitales cuyo número diario de nacimientos es múltiplo de cinco: 5, 10, 15, 20... 100. Lo son todos los que están, y están todos los que lo son.

Entre otras útiles características, los números que se pueden dividir por 5 exactamente, sin dejar resto, presentan la de tener un 60% entero, sin decimales. El de 5 es 3, el de 10, 6, el de 15, 9...., el de 150, 90..., el de 300, 180.

Son los únicos enteros a los que les pasa, además. Todos los demás números enteros, los no divisibles exactamente por cinco, tienen un 60% no entero, con una parte decimal más o menos larga. De todos los "sesentas por ciento" de los números enteros, solo los de los múltiplos de cinco son también números enteros, y van por el mundo sin arrastar una ristra de numeritos tras la coma.

(Es fácil entender por qué es así: 60% = 3/5. El sesenta por ciento de algo es lo mismo que tres quintas partes de ese algo. Si la quinta parte es un entero, al multiplicarla por tres da tambien un entero. Si no, malamente, porque el cinco y el tres son ambos primos y no tienen divisores comunes).

Lo de tener decimales no tiene por qué ser un problema para un número, en general. Conozco muchos números racionales, y hasta irracionales, que son muy felices siéndolo. (Aunque los que mejor se lo pasan, creo, son los imaginarios, si bien a veces tienen ciertos complejos). Solo empieza a ser algo delicado cuando se habla de partos, por ejemplo, o de niños. 

Si para alcanzar el 60% de varones sobre su total diario de nacimientos una clínica necesita dar a luz 2'4 niños, por ejemplo, porque en ella nacen 4 bebés al día ¿cómo hace? No puede detener el parto cuando asoman solo cuatro décimas partes de niño para señalar el histórico momento en que alcanza el umbral señalado. Menos aún puede amputarlas de los otros seis décimos de niño y declarar que con lo ya parido se da por satisfecha. Ni siquiera puede decidir que el recién nacido tiene de niño solo las cuatro partes necesarias para llegar al 60%, y que las otras seis que ya no hacen falta pueden ser de niña, si quieren.

Como adelanté hace un rato, ser niño o niña es un fenómeno discreto. Su variable tiene una unidad mínima e indivisible, es niño, o niña, entero, en bloque y con todos sus tres kilos y pico de peso. No hay bebés que tengan un 0'3457 de varón y el restante 0'6543 de hembra, o no al menos de modo que la comadrona pueda apreciarlo a simple vista y consignarlo en el estadillo con sus correspondientes decimales.

Si no fuera así, si los niños, o su condición de macho o hembra, fueran tan divisibles como conviniera, y su nacimiento y sexualidad, por tanto, un fenómeno de variable continua, todos los hospitales de nuestro problema situarían tranquilamente sus frecuencias de 60% de varones sobre la graciosa curva que marcan los máximos de nuestro dibujito, que es la que de verdad corresponde a ese umbral del 60%. Una vez alcanzado el número y pico de varón necesario, darían por cumplida su misión y pasarían tan contentos al siguiente parto, cuando lo hubiere. No habría dientes de sierra en nuestro problema, y yo no habría tenido que escribir estos tres terribles posts.

Pero es así, el sexo es una variable discreta, de unidad indivisible (como Ehpaña), y es por eso por lo que cuatro de cada cinco de los hospitales de nuestro problema, alcanzado el 60% de varones, tienen que seguir adelante con la criatura entera, dejar atrás el 60% y alcanzar, de hecho, otro umbral superior, cuya frecuencia de llegada es, por consiguiente, más baja. Y por ello no se sitúa sobre la curva que de verdad corresponde al umbral del 60%, la de los máximos, sino sobre otras curvas, más bajas, que corresponden a estos otros umbrales, más altos:

O, dicho de otro modo, las frecuencias que tanto nos han sobresaltado dibujando esa línea caprichosamente picuda solo corresponden al 60% en el caso de los máximos. Los otros cuatro hospitales de cada cinco están señalando en ella, en realidad, la frecuencia con la que alcanzan esos otros umbrales más altos a los que por fuerza tienen que llegar para ser "iguales o mayores" que el dichoso 60%. Frecuencias que, en exacto cumplimiento de las leyes estadísticas, son más bajas cuanto más alto sea ese otro umbral al que verdaderamente corresponden.

Arriba, en rojo, los umbrales (% de varones sobre el total de nacimientos) realmente alcanzados por cada hospital (siempre iguales o mayores que 60%). Abajo, en azul, las frecuencias con las que se alcanzan (% de días en los que se supera el umbral). Las líneas verticales permiten ver cómo a una subida en el umbral corresponde siempre una bajada en la frecuencia, y cómo a las frecuencias máximas les corresponde siempre el umbral del 60%. Como los umbrales se alejan cada vez menos de este límite inferior, las frecuencias se alejan cada vez menos de la curva de los máximos.

O sea, que mis cifras no pegaban saltos para desobedecer los principios de la Estadística, sino para ajustarse a ellos. Y nosotros, escandalizándonos.

Todo lo cual creo yo que nos permite dar por resuelta la cuestión y por suficientemente explicado el asunto. Confesemos que ya iba siendo hora.

Para terminar: el resultado es que estos hospitales en los que diariamente no nace un número de niños múltiplo de cinco desperdician buena parte de un niño para cumplir con la condición del problema. Este inevitable despilfarro de varonez, si quieren verlo así, baja su rendimiento y hace que superen el 60% de varones con una frecuencia inferior  a la que alcanzan otros hospitales, más ahorrativos por ser múltiplos de cinco sus números de nacimientos diarios.

Pero, sea cual sea el tamaño del hospital, la cantidad de varón así desperdiciada a los efectos de superar el 60% no llega en ninguno a un niño entero. El "sobrante" de masculinidad, en consecuencia, es cada vez menos importante en proporción al número total de nacimientos. No es lo mismo malgastar 0'6 niños de un total de 4 que malgastar 0'8 niños de un total de 182. El derroche va siendo proporcionalmente menor a medida que aumenta el número de nacimientos diario, y su incidencia sobre las frecuencias también. Los dientes de sierra de la curva, en resumen, son cada vez menos marcados.

Y hay que ver lo tranquilo que me he quedado yo.

La jornada de un obseso mental. Parte 2ª

Si no entiende usted nada de este post, debe tener en cuenta que se trata de la continuación de otro post, la 1ª parte. Si leída esta 1ª parte sigue sin entender nada, entonces ya sí puede estar seguro de que no es culpa suya.

Los síntomas se agravan.

Hay que decir en mi descargo que tuve cómplices. El culpable, o al menos el catalizador de esta y de algunas otras de mis afecciones mentales, puesto al tanto de mis indagaciones, decidió alentarlas enviándome una versión de mis hojas mejorada mediante el empleo de macros.

No me pregunten qué son las macros, porque no lo sé con exactitud. Tan solo que son una utilidad de las hojas de cálculo que aumenta vertiginosamente sus posibilidades. Les permite hacer cosas por su cuenta, en vez de limitarse a registrar las que hace el usuario, y en consecuencia las convierte en una especie de programas informáticos. Como tales, las macros son potencialmente peligrosas –quien las haya programado puede ser un avieso hacker que les haya ordenado hacer cosas "malas"– y Excel las trae deshabilitadas de fábrica. Para utilizarlas hay que habilitarlas primero en tu ordenador, y arriesgarte así a que te pase cualquier cosa después. Yo no las había usado nunca, e ignoro aún cómo se programan, aunque espero que no por mucho tiempo. Hay muuuchos fines de semana.

Por mi parte, lejos de contentarme con mis averiguaciones, me encontraba en plena fase maníaca y, abandonada toda mesura, me había dedicado también a mejorar mis hojas en la modesta medida de mis posibilidades. Ahora ya me permitían considerar hospitales de cualquier tamaño, no solo de 15 o 45 nacimientos diarios, sino de todos los posibles, desde 1 hasta 300. (Me pareció un límite razonable para un hospital, aunque no tengo ni idea de cuántos niños nacen cada día en uno de los grandes, La Paz o el Gregorio Marañon). Y podía también averiguar las frecuencias con que cualquiera de ellos alcanzaba o superaba no solo el umbral del 60% de niños, sino cualquier otro, desde el 50% hasta el 100%. Bastaba con introducir ambas variables en sendas casillas, sin necesidad de cambiar nada más en la hoja.

Así perfeccionada mi hoja con mis nuevas disposiciones y, sobre todo, con la macro de mi colaborador, la cosa era realmente sencilla. Fijabas el tamaño del hospital y el porcentaje de niños a superar, reseteabas y te ponías a simular año tras año, sin más que apretar  un botoncito para añadir un año más. Ya no era necesario apuntar trabajosamente en un papel aparte el resultado de cada año, para sumarlos luego y hallar su media. La hoja lo hacía por tí, iba sumando porcentajes anuales, dividiéndolos por el número de años y reflejando la media así hallada en una celda. Vean qué hermosura:

Armado de este prodigioso instrumento de aspecto engañosamente simple e inofensivo, y poseído de la perentoria necesidad de averiguar con qué frecuencia alcanzaba cada hospital los distintos umbrales, me apliqué, ávido, a darle al botón. Las cifras bailaban alegremente en la celda amarilla con cada nuevo clic. Se acabó el limitarse a 25 tristes años, ahora podía simular cuantos quisiera, 300, 400..., 1.000... sin más que un leve cansancio de dedo.

Digo que las cifras bailaban, y vaya si lo hacían. El último entero de la casilla amarilla se fijaba bastante pronto, pero los decimales seguían cambiando aún tras haber simulado doscientos años o más. Hasta los trescientos y pico golpes de dedo sobre el ratón no solía suceder que se estabilizara el primer decimal, que el segundo se decidiera a mantenerse en valores claramente mayores o menores que 5 y que yo pudiera juzgar, en consecuencia, que el porcentaje hallado empezaba a ser de fiar. Algunos recalcitrantes exigían cuatrocientos y hasta quinientos años antes de sentar la cabeza.

Trescientas y pico pulsaciones de índice sobre el ratón, pues, para cada uno de los trescientos tamaños de hospital posibles, y eso solo para averiguar las frecuencias con que alcanzaban el umbral del 60% de niños. Otros tantos si quisiera, además, conocer sus frecuencias para el 55% de niños, otros tantos para el 70%, otros tantos para el 80%...

No me importaba nada, estaba decidido a averiguar por vía empírica todo lo averiguable sobre la cuestión, así me costara un síndrome agudo del túnel carpiano.

(Mi mujer y mi hijo me observaban a distancia con cierta preocupación, cuchicheaban entre sí y me dirigían de vez en cuando, con gran prudencia, palabras de cariño y aliento a las que yo contestaba distraídamente. Acabaron decidiendo organizar su fin de semana sin contar conmigo).

(Pero el sábado salimos a cenar con unos amigos, y el domingo comimos con la familia, y superé ambas situaciones sin provocar comentarios. Quiero decir que, con todo, era capaz de mantener cierta fachada de normalidad).

Había un motivo para esta obsesión, es hora de decirlo. Al principio me había movido solo el deseo puramente deportivo de conseguir que mi hoja de cálculo fuera un buen simulador de nacimientos. Pero cuando empecé a registrar en una tabla los primeros resultados que me proporcionaba, descubrí con sobresalto que estos resultados hacían cosas por completo inesperadas.

Vean, si no, los cinco primeros porcentajes que mi hoja me había dado, y díganme si no es para sobresaltarse un poquito:

¡¡¡¡  !!!!

Se dan ustedes cuenta ¿no? Al subir de 1 a 2 nacimientos diarios, la frecuencia de días con un 60% de niños bajaba muy satisfactoriamente, del 50% al 25%. Hasta ahí, perfecto.

Pero al subir de 2 a 3 nacimientos diarios ¡la frecuencia subía también! ¡Otra vez al 50%!

Y no solo eso, sino que de 3 a 4 bajaba otra vez, sí, pero menos que había bajado para 2. Y con 5 nacimientos diarios, no solo volvía a subir hasta el 50% inicial, sino que lo superaba en cuatro décimas!⁽¹⁾

¡Pero qué estaba pasando aquí!

Tenía que haber un error. Algo en mi simulador no estaba funcionando como debía. Mi cómplice, sin duda, y sus peligrosas macros, habían estropeado mi Excelente invento. Volví a acumular clics como un poseso para obtener de nuevo los primeros resultados, pero la hoja insistió en darme las mismas o parecidas cifras.

Cuando la información es contradictoria, pensé, quizás solo sucede que nos falta información. Veamos qué sigue pasando con hospitales de tamaños mayores: en algún momento tendrán que asumir sus responsabilidades estadísticas y entrar en razón.

De modo que, suspendidas de momento las especulaciones teóricas, me apliqué con ahinco a darle al botoncillo y a registrar los resultados, absteniéndome de juzgarlos. Al cabo de... no sé realmente cuánto tiempo y de muchos clics, muchos miles de clics, mi tabla de porcentajes presentaba este anárquico aspecto:

No la he puesto entera porque es demasiado ancha y no se vería nada, pero llegué hasta el último hospital, el de 300 nacimientos diarios. Y al menos los cien primeros datos persistían en la insumisa e inexplicable manía de subir y bajar, en vez de acatar como debían la inequívoca ley estadística según la cual debían limitarse a bajar.

(Que a partir de 100 nacimientos diarios hubieran dejado de dar saltos no me consolaba nada: ese era el punto en que yo había empezado a aumentar los nacimientos de cinco en cinco, y no de uno en uno –el dedo, y el brazo entero, comenzaban a resentirse un poco–, así que con toda probabilidad solo sucedía que los saltos quedaban ocultos por esta omisión de cuatro de cada cinco hospitales, no que no siguieran produciéndose).

Porque, –y este era el único vislumbre lejano de que pudiera haber alguna explicación para el perturbador fenómeno– con todo y oscilar arriba y abajo de manera incomprensible, las frecuencias halladas parecían hacerlo con arreglo a alguna clase de patrón. Subían y bajaban contra todo pronóstico, sí, pero los picos parecía ser progresivamente menos altos, y los valles cada vez más bajos, y unos y otros daban la impresión de agruparse en ciclos de cierta regularidad.

Comprendí que, si algo de eso pasaba, se apreciaría más claramente en un dibujo, e hice que Excel trazara la correspondiente gráfica. Los gráficos siempre me han parecido una horterada para ejecutivos romos y exhibicionistas, y procuro no emplearlos salvo cuando son estrictamente necesarios, pero esta era claramente una de las ocasiones en que lo son:

Bien, así dibujada la cosa resultaba un poco menos caótica. Podía apreciarse un cierto método en aquella locura. A su manera, sí, a regañadientes, pero no había duda de que las frecuencias bajaban, aún haciéndolo con dos pasos hacia arriba y otros dos hacia abajo. En conjunto sí que se sometían, a fin de cuentas, a la ley que les ordenaba ser cada vez más pequeñas, aunque se reservaran el imprevisible derecho de hacerlo pegando unos tumbos que ninguna regla por mí conocida les autorizaba a pegar.

De momento era incapaz de encontrar ninguna razón que explicara su conducta, pero puesto que daba la impresión de atenerse a un cierto sistema, parecía posible que hubiera alguna. Solo era cuestión de dar con ella.

Con la trastienda del cráneo ocupada incesantemente en buscar esa explicación, me entretuve entretanto en localizar los máximos y mínimos locales del claudicante quebrado de líneas arriba, y en reflejarlos en el correspondiente dibujito. Más que otra cosa por explorar un poco las utilidades gráficas de Excel, que siempre he tenido muy abandonadas.

Y en hacer otro con las frecuencias con que algunos, (no todos, decididamente el brazo derecho empezaba a molestarme) de mis hospitales alcanzaban otros umbrales, concretamente el 55% y el 70% de varones . Para algo tenía que servir la brillante versatilidad de mi hoja de cálculo...

(Entre nosotros, no es que ninguno de estos dos gráficos me sirviera para gran cosa, pero tampoco se puede negar que tienen toda la pinta  de reflejar algo importante, y que prestan a este post un aspecto sumamente científico. Empiezo a comprender cómo funciona la cabeza de los ejecutivos romos y exhibicionistas...)

Por detrás de mis cavilaciones matemáticas y de mis divagaciones ilustratorias, empero, todo el rato runruneaba en mi cabeza una ocurrencia que me había asaltado al poco de empezar a registrar porcentajes, y de comprobar así lo errático de su comportamiento. Una ocurrencia tan subversiva e inquietante como innegable, una vez la hube comprobado en mi tabla de resultados. Era esta:

Si en vez de con dos hospitales de 45 y 15 nacimientos diarios, el problema se hubiera planteado con otros dos, por ejemplo, de 10 y 4 nacimientos diarios, la respuesta correcta ya no habría sido la canónica b), sino la a): sería el hospital grande el que registrara más días anuales con más del 60 % de varones.

Contravinendo todas las leyes estadísticas conocidas, pero con el irrefutable testimonio a favor de los porcentajes obtenidos con mi hoja de cálculo.

Y ello perturbaba gravemente mi conciencia matemática.

NOTAS

⁽¹⁾ Este 50'4% resultó ser un error de aproximación. Como veremos a su debido tiempo, la frecuencia con la que 5 nacimientos diarios alcanzan o superan el 60% de niños es exactamente del 50'0%. Las cuatro décimas de más se debieron sin duda a que, por una vez, no dí el suficiente número de clics y creí estabilizado el porcentaje antes de tiempo.

POST SCRIPTUM

Las reflexiones que este post ha inspirado a Miroslav, uno de mis cinco lectores, eran demasiado largas para un comentario, de lo que me siento satisfechísimo. De modo que ha decidido publicar su propio post sobre el asunto, o sobre algunos otros muy conectados con él. Ese post suyo, que Miroslav ha tenido la amabilidad de dedicarme, ha provocado a su vez algunas consideraciones mías que he publicado en forma de comentarios allí, pero que tienen mucho que ver con la cuestión que aquí se trata. 

La jornada de un obseso mental. Parte 1ª

Pormenorizado estudio de un lamentable cuadro clínico.

(Este post, para celebrar el renacimiento del blog tras más de un año de eclipse, no es apto para lectores no adictos a las matemáticas de andar por casa o, en su defecto, no interesados en problemas mentales de obsesión compulsiva).

Hace cosa de dos semanas me llegó una especie de adivinanza, acertijo, problema o como quieran ustedes llamarlo. Decía así: 

Una población tiene dos hospitales. En el hospital más grande nacen unos 45 bebés cada día, y en el más pequeño unos 15 bebés cada día. Como se sabe, alrededor del 50 por ciento de los bebés son niños. Pero el porcentaje exacto varía de un día a otro. Unas veces puede ser superior al 50 por ciento y otras, inferior. 

Durante un período de 1 año cada hospital registra los días en los que más del 60 por ciento de los bebés son niños. ¿Qué hospital crees que registró más días como estos? 

a) El hospital grande. 

 b) El hospital pequeño. 

c) Los dos más o menos lo mismo (es decir, con una diferencia del 5 por ciento entre uno y otro). 

Me pilló con la cabeza en otras cosas y estuve un par de días sin hacerle ni caso. Cuando decidí hacérselo contesté al remitente, tras pensar dos minutos, algo así como: "No veo ningún motivo para que ninguno de los dos tenga más días con un 60 % de varones que el otro, así que imagino que la respuesta correcta es la c). Lo que me desconcierta es que se plantee como problema, a mí me parece obvio. Pero puesto que me lo preguntas, debe de ser que no lo es tanto. Se me debe de estar escapando algo, pero no sé qué."

Me desasosiega mucho la sensación de que algo se me está escapando, así que el problema siguió dándome vueltas dentro de la cabeza. Hasta que para acabar con mi desazón decidí llevarlo a los extremos, que suele ser una excelente manera de razonar (tiene el inconveniente de que nunca falta quien te llame exagerado, o asegure que eso que tú dices no tiene nada que ver con lo que ha dicho él, o te acabe acusando, con virtuosa indignación, de hacer comparaciones escandalosas y ofensivas entre, qué sé yo, la tauromaquia y la ablación del clítoris, por ejemplo. Pero no hay que hacer caso, yo ya estoy acostumbrado y persevero en practicar la reductio ad extremum, que me resulta siempre muy esclarecedora).

Imaginemos otros dos hospitales, más diferentes aún que los del problema, me dije a mí mismo. Uno tan pequeño que solo nazca en él un niño al día y otro tan grande que nazcan cinco mil. ¿Superarán los dos con la misma frecuencia el 60% de nacimientos de un sexo determinado?

Y una vez más, en los extremos se me hizo la luz: el pequeño alcanzará un 60% de varones –lo superará, de hecho, con el 100%–  todos los días en los que su único alumbramiento diario sea niño, es decir, más o menos la mitad de los días. En cambio el enorme es seguro que no lo alcanzará nunca. Es estadísticamente imposible que de cinco mil bebés, tres mil sean varones. Lo previsible es que se repartan por mitades, 2.500 machos y 2.500 hembras. En la práctica, claro, el reparto nunca será tan exacto, puede suceder que un día haya 2.550 niños y 2.450 niñas, o viceversa. Puedo llegar, en un día loco, –con luna llena, o nueva, o como tenga que estar para estas cosas–, a 2.600 de un sexo contra 2.400 del otro, y ya me parece mucho conceder. Pero por muy imprevistamente que la realidad quiera sacudirse las tutelas estadísticas que la apacientan, lo que evidentemente no sucederá nunca en este hospital enorme es que nazcan 3.000 de un sexo y solo 2.000 del otro; y eso es lo que tendría que pasar para que se alcanzara el 60 % de nuestro problema.⁽¹⁾

O sea, que en el de 1 nacimiento diario se alcanzará el 60% de varones ciento ochenta y tantos días al año. Y en el de 5.000, ni un solo día. La cosa parece clara.

Cuanto más grande sea el hospital y más nacimientos se produzcan en él, más se ceñirán estos nacimientos al reparto esperable entre varones y hembras, que es del 50 % para cada uno, y menos probabilidad habrá de que las desviaciones diarias de esa media sean significativas. Por lo que el hospital grande, de cuarenta y cinco nacimientos diarios, registrará un 60 % o más de varones menos días que el hospital pequeño, de solo quince. La respuesta correcta, comprendí, es la b): el hospital pequeño.

(Es el mismo principio, evidente una vez caes en él, por el que las encuestas son más fiables cuantas más encuestados haya. Si tú le preguntas a diez o doce vecinos lo que piensan votar, el resultado de tu consulta no se parecerá ni de lejos al de las elecciones. Si se lo pudieras preguntar a la mitad del censo, lo clavarías.)

Pero a pesar de mi natural satisfacción por haberme demostrado a mí mismo una vez más lo listo que soy –aunque, eso sí, un poco lento– quedaba un detalle que seguía rondándome por la cabeza. El enunciado del problema hablaba de que hubiera entre los dos hospitales una diferencia de menos del 5 %. Y yo no sabía si ese requisito se cumplía. El hospital de quince nacimientos diarios tendrá más días fastos –o nefastos, según se mire– que el de cuarenta y cinco, de acuerdo, pero ¿cuántos más? Porque si en uno es esperable que se registren... por ejemplo... treinta y cinco días al año con más del 60 % de varones, y en el otro solo treinta y cuatro días al año, esta diferencia cumplirá la regla general de que el pequeño sea estadísticamente más díscolo, pero la respuesta al problema ya no será la b), sino la c), porque la diferencia entre ambos no llegará al 5 %.

Me volví loco buscando por Internet alguna regla estadística que relacionara el tamaño de una muestra (el número diario de nacimientos) con las varianzas, desviaciones típicas o cualquier otra magnitud que mida las diferencias esperables entre los datos reales y la media a la que deberían aproximarse. No creo que exista –lo ignoro todo de la Estadística y casi todo del Cálculo de Probabilidades– pero, en cualquier caso, no la encontré, como era de esperar.

Puesto que la predicción teórica me falla, me dije muy científicamente, recurramos a la comprobación empírica. No puede ser muy difícil hacer con Excel un simulador de nacimientos, niño o niña, y comprobar cuántos días de cada trescientos sesenta y cinco uno de estos dos sexos alcanza o supera el 60% si los hacemos nacer de quince en quince, y cuántos si los hacemos nacer de cuarenta y cinco en cuarenta y cinco.

Soy un poco raro, y pocas cosas (algunas, sí, tranquilos: pero pocas) me entretienen y absorben más que inventarme hojas de Excel para propósitos recónditos y tirando a abstrusos Las hojas de cálculo me parecen la herramienta más asombrosamente útil que nos ha dado la informática a los ciudadanos de a pie –con la posible excepción del FinaleNotepad–. No soy un experto en su uso, manejo con cierta soltura las funciones más básicas, pero precisamente por eso me fascina explorar el enorme campo de sus posibilidades que aún desconozco, y haciéndolo a mi aire es, en realidad, como he llegado a la modesta destreza con que las empleo. Puedo estarme horas trasteando con ellas hasta conseguir que hagan lo que pretendo. Nunca he entendido, por eso, que nadie se gaste un duro de su dinero ni dos minutos de su tiempo en juegos ni en videoconsolas, teniendo un Excel diez veces más apasionante que el mejor de ellos.

Así que al cabo de media horita, o quizás menos, de pensar intensamente y de investigar funciones de Excel ya tenía a punto mi simulador. La función "=aleatorio()" te da, en cada casilla en que la metas, un número decimal entre 0 y 1, uno cualquiera al azar entre los mil billones⁽²⁾ posibles, todos de la forma "0,453625885714902". Si la metes en quince casillas, y a cada una de ellas le das el valor "1" cuando el numerito en cuestión sea mayor o igual que 0'5, y el valor "0" cuando sea menor, tienes quince fenómenos aleatorios, cada uno de ellos con dos opciones, "0" o "1", de igual probabilidad. Es decir, quince lanzamientos de moneda a cara o cruz. O quince nacimientos a niño o niña: una exacta reproducción de un día de la clínica pequeña.

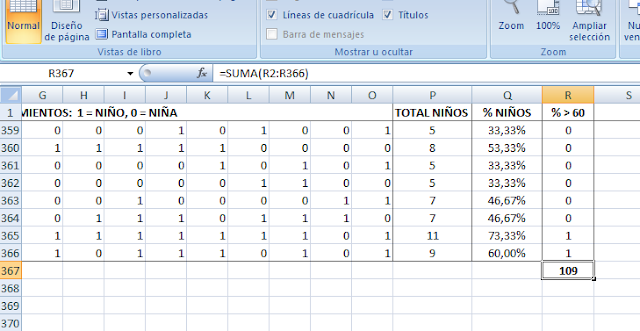
Si en una decimosexta casilla sumas el contenido de las quince anteriores, sabes cuántos niños ("1") han nacido ese día (o cuántas niñas, si hubieras decidido que el "1" son niñas; no quiero herir suceptibilidades feministas). Si en otra decimoséptima casilla divides ese número de niños por quince, sabes qué porcentaje de niños ("1") ha habido ese día sobre el total de nacimientos. Y si en otra decimoctava casilla haces aparecer un "1" si ese porcentaje es igual o mayor que 0'6, y un "0" si es menor, ya tienes cuantificado uno de tus días, como fasto ("1") o como nefasto ("0").

Basta repetir, copiando y pegando, este mismo esquema en otras trescientas sesenta y cuatro filas para tener un año de la clínica pequeña. En la fila tricentésimo sexagésimo sexta (la número 366, vaya, o la número 367 si se emplea una primera fila en encabezamientos aclaratorios, como yo hice) sumas los días (filas) fastos, y ya sabes cuántos días de ese año el sexo elegido ha alcanzado o superado el 60% de los nacimientos. Cada vez que actualices la hoja con F9, tienes un nuevo año, con su numerito de días "especiales". Y si lo haces una cantidad razonable de veces, apuntas los resultados, los sumas y divides el total por esa cantidad, tienes la media de todos los años así simulados: una aproximación más o menos fiable de lo que cabe esperar que produzca anualmente la clínica pequeña en cuestión de días con más del sesenta por ciento de niños de un sexo determinado.

Veinticinco años nada más simulé yo, porque apuntar el resultado cada vez que "actualizaba" a un nuevo año era una pesadez, y sumar luego los resultados, otra peor. Veinticinco años me parecieron suficiente muestra –y suficiente trabajo–, y me salieron 110 días al año de media, en ese primer y trabajoso recuento. Más o menos, el 30 % de los días.⁽³⁾

Y haciendo lo mismo en otra hoja para el hospital grande (la cosa se hace exactamente igual, cambiando quince por cuarenta y cinco: metes la fórmula en cuarenta y cinco casillas, divides por cuarenta y cinco la suma de "unos"... y el resto, igual que en la otra) resultó que en ella la cosa andará, más o menos, en torno a los 43 días al año con más del sesenta por ciento de nacimientos de un sexo determinado: entre el 11 y el 12 % de los días.

Asunto resuelto.

Cabría esperar que con todo esto el obseso mental que hay en mí se quedara tranquilo: la diferencia prevista por la teoría se cumplía muy satisfactoriamente en la práctica, y muy holgadamente, además. Había mucho más de un 5% de distancia entre las frecuencias con las que una y otra clínica superaban el umbral del 60% de varones. Ya podía responder con seguridad que la respuesta correcta era la b) y olvidarme del asunto. 

Pero, amigos míos, la dolencia era más grave de lo que parecía a primera vista, y el adicto no había hecho más que empezar a adentrarse en los infiernos de su vicio.

Lo que quiere decir, tiemblen, que nos espera al menos una segunda parte...

⁽¹⁾ Una simulación con Excel de un hospital de 5.000 nacimientos diarios durante 2.500 días no arrojó ni un solo día con más de 2.680 niños de uno de los dos sexos. La máxima desviación producida sobre el 50% esperable fue el 53'5% (2.673 niños del mismo sexo). A mi ordenador, eso sí, le llevó un ratito el averiguarlo.

⁽²⁾ Mil billones, claro, si solo consideramos los quince primeros decimales, como hace Excel. En realidad son infinitos. Qué fatiga...

⁽³⁾ No olvidemos que, presumible y simétricamente, habrá otro treinta por ciento de días en que los varones nacidos no alcancen el 40%, es decir, en que lo que alcance o supere el 60% sea el nacimiento de niñas. O sea, que el porcentaje de días en que alguno de los dos sexos alcance o supere el 60%  será el doble del hallado para un sexo determinado. En este caso, del sesenta por ciento, y en el de la clínica grande, del veintitantos por ciento. Podría hacer una hoja que calculara también esta frecuencia...